Interested Article - Поле Киллинга

- 2021-08-06
- 1
По́ле Ки́ллинга (в теории относительности часто просто ве́ктор Ки́ллинга ) — векторное поле скоростей (локальной) однопараметрической группы движений риманова или псевдориманова многообразия .
Другими словами, поток, который генерируется векторным полем Киллинга, задаёт непрерывное однопараметрическое семейство движений многообразия, то есть преобразований, относительно которых метрический тензор остаётся инвариантным.
В частности, если метрический тензор в некоторой системе не зависит от одной из координат , тогда векторное поле вдоль этой координаты будет полем Киллинга.
Векторы Киллинга в физике указывают на симметрию физической модели и помогают найти сохраняющиеся величины, такие как энергия , импульс или спин . В теории относительности , например, если метрический тензор не зависит от времени, то в пространстве-времени существует времениподобный вектор Киллинга, с которым связана сохраняющаяся величина — энергия гравитационного поля.
Название дано в честь немецкого математика Вильгельма Киллинга , открывшего группы Ли и многие их свойства параллельно с Софусом Ли .
Определение
Векторное поле на называется полем Киллинга если оно удовлетворяет следующему уравнению:
где — производная Ли по направлению , a — риманова метрика на .
Это уравнение можно переписать через связность Леви-Чивиты :
для любых полей и .
В терминах локальных координат:
Свойства
- Векторное поле является полем Киллинга тогда и только тогда, когда сужение на любую геодезическую является полем Якоби .
- Для задания поля Киллинга достаточно указать его значение, плюс значения всех его ( ковариантных ) производных первого порядка, всего в одной точке. Из этой точки векторное поле может быть продолжено на всё многообразие.
- Скобка Ли , или коммутатор, двух полей Киллинга даёт опять поле Киллинга. Таким образом, поля Киллинга образуют подалгебру бесконечномерной алгебры Ли всех (дифференцируемых) векторных полей на многообразии . Эта подалгебра является алгеброй Ли группы движений многообразия.
-
Линейная комбинация
полей Киллинга тоже является полем Киллинга.
-
Иллюстрация сложения полей Киллинга на плоскости. Поле вращений вокруг начала координат + поле
параллельного переноса
вдоль оси
y
= поле вращений вокруг центра, смещённого относительно начала координат вдоль оси
x
:
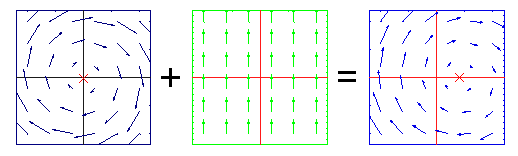
Все три поля являются полями движений плоскости.
-
Иллюстрация сложения полей Киллинга на плоскости. Поле вращений вокруг начала координат + поле
параллельного переноса
вдоль оси
y
= поле вращений вокруг центра, смещённого относительно начала координат вдоль оси
x
:
- Если кривизна Риччи компактного многообразия отрицательна, то на нём нет нетривиальных (то есть не равных тождественно нулю) полей Киллинга.
- Если секционная кривизна компактного многообразия положительная и размерность чётная, то поле Киллинга должно иметь нуль.
Примеры
- На евклидовой плоскости существует три линейно независимых поля Киллинга:
-
- , ,
- Первые два поля Киллинга отвечают сдвигов вдоль осей и , а последнее — подгруппе вращений вокруг начала координат. Различные комбинации из этих трёх подгрупп исчерпывают всевозможные движения плоскости.
- В трёхмерном евклидовом пространстве существует шесть линейно независимых полей Киллинга:
-
- , ,
- Последние три поля , и являются также полями Киллинга на сфере (это становится очевидным если рассматривать её погруженной в трёхмерное пространство ).
- Однолистный гиперболоид , задаваемый уравнением , погружённый в пространство Минковского с метрикой , имеет три линейно независимых поля Киллинга, подобных полям Киллинга на сфере:
Вариации и обобщения
- Конформные поля Киллинга , определяются формулой
-
- для некоторого скаляра . Они являются производными однопараметрических семейств конформных отображений .
- Конформные тензорные поля Киллинга : симметричные тензорные поля , такие что симметризация равна нулю.
- Антисимметричное тензорное поле Киллинга — Яно , часто представляемое, как «корень квадратный из симметричного тензорного поля Киллинга». Симметрия, описываемая тензорами Киллинга и Киллинга — Яно, существует во вращающихся чёрных дырах Керра , а также некоторых их обобщениях. Наличие подобной симметрии объясняет, почему разделяются переменные в уравнениях движения классической и квантовой релятивистской механики : Гамильтона — Якоби , волновом , Клейна — Гордона , Дирака и др.
- Тензорное поле Киллинга .
Примечания
- . Квантовые частицы в полях Эйнштейна — Максвелла/Кишинев. Штиинца. 1989.
Литература
- Рашевский П. К. Риманова геометрия и тензорный анализ — М.: Наука, 1967.
- Эйзенхарт Л. П. Риманова геометрия — М.: Изд-во иностр. лит., 1948.
- Xелгасон С. Дифференциальная геометрия и симметрические пространства — М.: Мир, 1964.
- Кобаяси Ш., Номидзу К. Основы дифференциальной геометрии — М.: Наука, 1981.
- 2021-08-06
- 1























































































