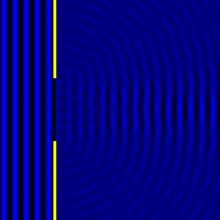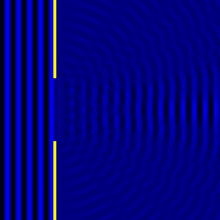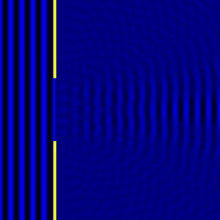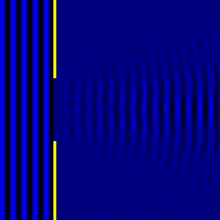
Дифракция на двух щелях красного лазера
Дифракция на двух и пяти щелях
Распространение волны через щель шириною в длину волны.
Распространение волны через щель, превосходящую шириною длину волны в шесть раз.
Численное приближение дифракционной картины для щели шириной в четыре длины волны с падающей плоской волной. Видны центральный луч, нули, изменение фазы на
π
{\displaystyle \pi }
График и вид дифракции на одной щели.
Дифракция на N щелях
— это частная задача оптики, где рассматривается дифракция на нескольких щелях в непроницаемом экране.
Рассмотрим сначала математическое представление
принципа Гюйгенса
:
Ψ
=
∫
s
l
i
t
i
r
λ
Ψ
′
e
−
i
k
r
d
s
l
i
t
{\displaystyle \Psi =\int _{slit}{\frac {i}{r\lambda }}\Psi ^{\prime }e^{-ikr}\,dslit}
Рассмотрим
N
щелей в экране с равными ширинами (
a
,
∞
{\displaystyle \infty }
d
между ними вдоль оси x′. Расстояние
r
от первой щели задаётся формулой:
r
=
z
(
1
+
(
x
−
x
′
)
2
+
y
′
2
z
2
)
1
2
{\displaystyle r=z\left(1+{\frac {\left(x-x^{\prime }\right)^{2}+y^{\prime 2}}{z^{2}}}\right)^{\frac {1}{2}}}
Для обобщения на
N
щелей, заметим, что
z
и
y
остаются постоянными, когда x′ сдвигается на
x
j
=
0
⋯
n
−
1
′
=
x
0
′
−
j
d
{\displaystyle x_{j=0\cdots n-1}^{\prime }=x_{0}^{\prime }-jd}
Таким образом,
r
j
=
z
(
1
+
(
x
−
x
′
−
j
d
)
2
+
y
′
2
z
2
)
1
2
{\displaystyle r_{j}=z\left(1+{\frac {\left(x-x^{\prime }-jd\right)^{2}+y^{\prime 2}}{z^{2}}}\right)^{\frac {1}{2}}}
и сумма по всем
N
вкладам в амплитуду:
Ψ
=
∑
j
=
0
N
−
1
C
∫
−
a
2
a
2
e
i
k
x
(
x
′
−
j
d
)
z
e
−
i
k
(
x
′
−
j
d
)
2
2
z
d
x
′
{\displaystyle \Psi =\sum _{j=0}^{N-1}C\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{\frac {ikx\left(x^{\prime }-jd\right)}{z}}e^{\frac {-ik\left(x^{\prime }-jd\right)^{2}}{2z}}\,dx^{\prime }}
Замечая, что величина
k
(
x
′
−
j
d
)
2
z
{\displaystyle {\frac {k\left(x^{\prime }-jd\right)^{2}}{z}}}
e
−
i
k
(
x
′
−
j
d
)
2
2
z
≈
1
{\displaystyle e^{\frac {-ik\left(x^{\prime }-jd\right)^{2}}{2z}}\approx 1}
Ψ
{\displaystyle \Psi }
=
C
∑
j
=
0
N
−
1
∫
−
a
2
a
2
e
i
k
x
(
x
′
−
j
d
)
z
d
x
′
{\displaystyle =C\sum _{j=0}^{N-1}\int _{-{\frac {a}{2}}}^{\frac {a}{2}}e^{\frac {ikx\left(x^{\prime }-jd\right)}{z}}\,dx^{\prime }}
=
C
∑
j
=
0
N
−
1
(
e
i
k
a
x
2
z
−
i
j
k
x
d
z
−
e
−
i
k
a
x
2
z
−
i
j
k
x
d
z
)
2
i
k
a
x
2
z
{\displaystyle =C\sum _{j=0}^{N-1}{\frac {\left(e^{{\frac {ikax}{2z}}-{\frac {ijkxd}{z}}}-e^{{\frac {-ikax}{2z}}-{\frac {ijkxd}{z}}}\right)}{\frac {2ikax}{2z}}}}
=
C
∑
j
=
0
N
−
1
e
i
j
k
x
d
z
(
e
i
k
a
x
2
z
−
e
−
i
k
a
x
2
z
)
2
i
k
a
x
2
z
{\displaystyle =C\sum _{j=0}^{N-1}e^{\frac {ijkxd}{z}}{\frac {\left(e^{\frac {ikax}{2z}}-e^{\frac {-ikax}{2z}}\right)}{\frac {2ikax}{2z}}}}
=
C
sin
k
a
sin
θ
2
k
a
sin
θ
2
∑
j
=
1
N
−
1
e
i
j
k
d
sin
θ
{\displaystyle =C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}\sum _{j=1}^{N-1}e^{ijkd\sin \theta }}
Теперь используем следующее равенство:
∑
j
=
0
N
−
1
e
x
j
=
1
−
e
N
x
1
−
e
x
.
{\displaystyle \sum _{j=0}^{N-1}e^{xj}={\frac {1-e^{Nx}}{1-e^{x}}}.}
Подставляя в наше уравнение, приходим к выражению:
Ψ
{\displaystyle \Psi }
=
C
sin
k
a
sin
θ
2
k
a
sin
θ
2
(
1
−
e
i
N
k
d
sin
θ
1
−
e
i
k
d
sin
θ
)
{\displaystyle =C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}\left({\frac {1-e^{iNkd\sin \theta }}{1-e^{ikd\sin \theta }}}\right)}
=
C
sin
k
a
sin
θ
2
k
a
sin
θ
2
(
e
−
i
N
k
d
sin
θ
2
−
e
i
N
k
d
sin
θ
2
e
−
i
k
d
sin
θ
2
−
e
i
k
d
sin
θ
2
)
(
e
i
N
k
d
sin
θ
2
e
i
k
d
sin
θ
2
)
{\displaystyle =C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}\left({\frac {e^{-iNkd{\frac {\sin \theta }{2}}}-e^{iNkd{\frac {\sin \theta }{2}}}}{e^{-ikd{\frac {\sin \theta }{2}}}-e^{ikd{\frac {\sin \theta }{2}}}}}\right)\left({\frac {e^{iNkd{\frac {\sin \theta }{2}}}}{e^{ikd{\frac {\sin \theta }{2}}}}}\right)}
=
C
sin
k
a
sin
θ
2
k
a
sin
θ
2
e
−
i
N
k
d
sin
θ
2
−
e
i
N
k
d
sin
θ
2
2
i
e
−
i
k
d
sin
θ
2
−
e
i
k
d
sin
θ
2
2
i
(
e
i
(
N
−
1
)
k
d
sin
θ
2
)
{\displaystyle =C{\frac {\sin {\frac {ka\sin \theta }{2}}}{\frac {ka\sin \theta }{2}}}{\frac {\frac {e^{-iNkd{\frac {\sin \theta }{2}}}-e^{iNkd{\frac {\sin \theta }{2}}}}{2i}}{\frac {e^{-ikd{\frac {\sin \theta }{2}}}-e^{ikd{\frac {\sin \theta }{2}}}}{2i}}}\left(e^{i(N-1)kd{\frac {\sin \theta }{2}}}\right)}
=
C
sin
(
k
a
sin
θ
2
)
k
a
sin
θ
2
sin
(
N
k
d
sin
θ
2
)
sin
(
k
d
sin
θ
2
)
e
i
(
N
−
1
)
k
d
sin
θ
2
{\displaystyle =C{\frac {\sin \left({\frac {ka\sin \theta }{2}}\right)}{\frac {ka\sin \theta }{2}}}{\frac {\sin \left({\frac {Nkd\sin \theta }{2}}\right)}{\sin \left({\frac {kd\sin \theta }{2}}\right)}}e^{i\left(N-1\right)kd{\frac {\sin \theta }{2}}}}
поставим
k
в виде
2
π
λ
{\displaystyle {\frac {2\pi }{\lambda }}}
I
0
{\displaystyle I_{0}}
на одной щели
. Помня
⟨
e
i
x
|
e
i
x
⟩
=
e
0
=
1
{\displaystyle \langle e^{ix}{\Big |}e^{ix}\rangle \ =e^{0}=1}
I
(
θ
)
=
I
0
[
sinc
(
π
a
λ
sin
θ
)
]
2
⋅
[
sin
(
N
π
d
λ
sin
θ
)
sin
(
π
d
λ
sin
θ
)
]
2
{\displaystyle I\left(\theta \right)=I_{0}\left[\operatorname {sinc} \left({\frac {\pi a}{\lambda }}\sin \theta \right)\right]^{2}\cdot \left[{\frac {\sin \left({\frac {N\pi d}{\lambda }}\sin \theta \right)}{\sin \left({\frac {\pi d}{\lambda }}\sin \theta \right)}}\right]^{2}}
.
, 0) и расстояниями
d
между ними вдоль оси x′. Расстояние
r
от первой щели задаётся формулой:
мала при рассмотрении дифракции Фраунгофера, и
, получим:
и представляя все неосциллирующие постоянные как
, как в дифракции
, получим для интенсивности света ответ:
![{\displaystyle I\left(\theta \right)=I_{0}\left[\operatorname {sinc} \left({\frac {\pi a}{\lambda }}\sin \theta \right)\right]^{2}\cdot \left[{\frac {\sin \left({\frac {N\pi d}{\lambda }}\sin \theta \right)}{\sin \left({\frac {\pi d}{\lambda }}\sin \theta \right)}}\right]^{2}}](/images/000/504/504580/30.jpg?rand=284190)
gaynor
