Interested Article - Куб
Куб ( др.-греч. ); иногда гекса́эдр или правильный гекса́эдр — многогранник, поверхность которого состоит из шести квадратов . Куб является правильным многогранником . Частный случай параллелепипеда и призмы .
В различных дисциплинах используются значения термина, имеющие отношения к тем или иным свойствам геометрического прототипа. В частности, в аналитике ( OLAP -анализ) применяются так называемые аналитические многомерные кубы , позволяющие в наглядном виде сопоставить данные из различных таблиц.
Содержание
Свойства куба
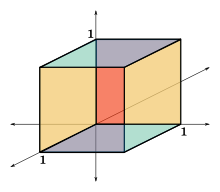
- Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
- В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трёхгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным, а его объём составляет 1/3 от объёма куба.
- В куб можно вписать октаэдр , притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
- Куб можно вписать в октаэдр , притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
- В куб можно вписать икосаэдр , при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
-
Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Длина
 диагонали куба с ребром
диагонали куба с ребром
 находится по формуле
находится по формуле

См. также
Примечания
- (неопр.) . Дата обращения: 7 октября 2018. Архивировано из 28 декабря 2014 года.
- Справочник по элементарной математике / Выгодский М. Я. . — М. : АСТ , Астрель , 2006. — С. 383—384.
- Англо-русский словарь математических терминов / под ред. П. С. Александрова . — 2-е, исправл. и дополн. изд.. — М. : Мир , 1994. — С. 129. — 416 с. — ISBN 5-03-002952-4 .
- Гексаэдр // Математическая энциклопедия / И. М. Виноградов . — 1977. — Т. 1.
- Энциклопедия элементарной математики. Книга 4 (геометрия) / П. С. Александров , А. И. Маркушевич , А. Я. Хинчин . — ГИФМЛ , 1963. — С. 426.
Ссылки
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- *
- , with interactive animation
|
|
|
|---|---|
| Многоугольники | |
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
|
Правильные многогранники
и сферические паркеты |
|
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники | |
|
|
Это
заготовка статьи
по
математике
. Помогите Википедии, дополнив её.
|
- Tags: