Interested Article - Замощение (геометрия)

- 2020-03-27
- 1

Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.
Кроме паркетов на евклидовой плоскости , в математике рассматриваются «паркеты» на сфере , гиперболической плоскости , в трёхмерном и многомерном пространстве.
Терминология
Замощения, мозаики, паркеты, разбиения
Паркеты иначе называются замощениями , мозаиками ( англ. tessellation, tiling ), разбиениями плоскости ( англ. partition ), паркетажами . Замощения трёхмерного пространства и пространств высших размерностей часто называют со́тами .
На странице 16 книги Грюнбаума и «Tilings and Patterns» (1987) находится следующее примечание:
В математической литературе слова tessellation , paving , mosaic и parquetting используются как синонимы или со сходными значениями. Немецкие слова для мозаики — Pflasterung , Felderung , Teilung , Parkettierung и Zerlegung ; французские слова — pavage , carrelage и dallage ; русские слова — паркетаж , разбиение и замощение .
Оригинальный текст (англ.)In mathematical literature, the words tessellation , paving , mosaic and parquetting are used synonymously or with similar meanings. The German words for tiling are Pflasterung , Felderung , Teilung , Parkettierung and Zerlegung . The French words are pavage , carrelage and dallage . The Russian words are паркетаж , разбиение and замощение .
Паркеты с областями (плитками) произвольной формы иногда называют картами (см., напр., теорема о четырёх красках ).
Покрытия и упаковки
Если объединение нескольких фигур содержит данную фигуру Ф , то говорят, что эти фигуры образуют покрытие фигуры Ф . При этом покрывающие фигуры могут перекрываться, но покрывают фигуру Ф без пробелов.
— это размещение внутри данной фигуры нескольких фигур, не имеющих общих точек, кроме, быть может, граничных (т.е. без перекрытий).
Замощение — это разбиение фигуры на части. Замощение является одновременно покрытием и упаковкой .


Протоплитки
Протоплитки паркета ( англ. prototiles , также прототипы ) — это плитки (формы), входящие в паркет. Каждая плитка паркета конгруэнтна одной из протоплиток .
Так, единственная протоплитка шестиугольного паркета — правильный шестиугольник; протоплиткой правильного сферического пятиугольного паркета является пентагон ; множество протоплиток ромботришестиугольного паркета состоит из равностороннего треугольника, квадрата и гексагона .
Паркет называется k -эдрическим, если множество его протоплиток ( протомножество ) состоит из k плиток .
Плитки паркета также называют гранями , а стороны многоугольных плиток — рёбрами , по аналогии с терминологией для многогранников .


Конфигурации вершин и граней
состоит из плиток трёх типов: равносторонний треугольник, квадрат и гексагон . Эти плитки располагаются вокруг каждой из вершин в следующем порядке: треугольник, квадрат, шестиугольник, квадрат. Такой порядок называется конфигурацией вершины паркета и записывается в форме 3.4.6.4. В случае, если два и более числа в этой последовательности идут подряд, используется сокращённая запись: треугольный паркет может быть обозначен как 3.3.3.3.3.3 или как 3 6 . При этом записи, отличающиеся лишь циклической перестановкой чисел или изменением порядка записи на противоположный (например, 3.3.4.3.4 и 4.3.3.4.3), обозначают одну и ту же конфигурацию вершины; в то же время запись 3.4.4.6 не эквивалентна записи 3.4.6.4 .
В неоднородных паркетах могут встречаться вершины с разными конфигурациями.
Конфигурацией грани называется последовательность степеней вершин этой грани при обходе её в одном направлении. Конфигурация грани записывается последовательностью чисел в квадратных скобках или с префиксом V.
Если все вершины некоторого паркета имеют одну и ту же конфигурацию с записью a 1 .a 2 ....a k , то все грани двойственного ему паркета имеют одну и ту же конфигурацию с записью Va 1 .a 2 ....a k . Например, конфигурации граней (англ.) , записываются как V3.4.6.4.
Виды паркетов
Во многих случаях принимается условие эквивалентности каждой из протоплиток паркета ; иными словами, плитка не должна состоять из нескольких частей ( квазиполимино ), содержать «отверстия», быть и т.п. .
Паркеты на плоскости
Правильные паркеты
Паркеты, составленные из одинаковых правильных многоугольников, называют правильными паркетами ( англ. regular tilings ). Существует три правильных замощения плоскости: треугольный паркет , квадратный паркет и шестиугольный паркет .
- Правильные паркеты
-

-

-

Правильные паркеты называют также платоновыми паркетами .
Полиформы , располагающиеся на правильных паркетах, называются соответственно полиамондами , полимино и полигексами .
Для обозначения паркета из правильных p -угольников, расположенных по q вокруг каждой вершины, применяется символ Шлефли { p , q }. Символы Шлефли трёх правильных мозаик — {3,6}, {4,4} и {6,3} .
Полуправильные паркеты
Паркеты, состоящие из правильных многоугольников двух или более типов, такие, что для любых двух вершин паркета существует преобразование симметрии (самосовмещение), переводящее одну из них в другую, называются полуправильными паркетами ( англ. semiregular tilings ) или архимедовыми паркетами .
Существует 8 полуправильных паркетов . Один из восьми полуправильных паркетов ( курносый тришестиугольный паркет ) является хиральным , то есть не совпадает с собственным зеркальным отражением .
- Полуправильные паркеты (Архимедовы паркеты)
-

-
 Курносый квадратный паркет
Курносый квадратный паркет
3.3.4.3.4 -
 Тришестиугольный паркет
Тришестиугольный паркет
3.6.3.6 -
![Усечённый шестиугольный паркет[en] 3.12.12](/images/005/071/5071915/14.jpg?rand=198428)
3.12.12 -
![Ромботришестиугольный паркет[en] 3.4.6.4](/images/005/071/5071915/15.jpg?rand=522993)
3.4.6.4 -
![Ромбоусечённый тришестиугольный паркет[en] 4.6.12](/images/005/071/5071915/16.jpg?rand=198733)
4.6.12 -
![Изокурносый треугольный паркет[en] 3.3.3.4.4](/images/005/071/5071915/17.jpg?rand=233013)
3.3.3.4.4 -

Существует два определения, приводящих к одному и тому же набору из 8 полуправильных паркетов на плоскости.
Первое, «локальное» определение, заключается в том, что вершинные конфигурации всех вершин должны совпадать. Иными словами, последовательности граней вокруг любых двух вершин паркета должны быть одинаковыми: одни и те же многоугольники должны идти в одном и том же (или в противоположном) порядке.
Второе, «глобальное» определение, требует, чтобы для любых двух вершин паркета существовало преобразование симметрии (самосовмещение паркета), переводящее одну из них в другую.
Грюнбаум и Шепард разделяют термины «архимедов паркет» ( англ. Archimedean tiling ) и « однородный паркет » ( англ. uniform tiling ): к первой группе относятся паркеты, соответствующие «локальному» определению, а ко второй — «глобальному». Хотя на евклидовой плоскости два этих множества совпадают, в других пространствах существуют архимедовы паркеты, не являющиеся однородными .
В математической литературе значения терминов «архимедов паркет», «полуправильный паркет» и «однородный паркет» варьируются.



Квазиправильные паркеты
Квазиправильный паркет (или многогранник) ( англ. quasiregular tiling ) — однородный паркет (или многогранник), состоящий из граней двух видов, чередующихся вокруг каждой вершины; иными словами, каждая грань окружена гранями другого типа .
На евклидовой плоскости существует лишь один квазиправильный паркет — тришестиугольный паркет с вершинной конфигурацией 3.6.3.6. На сфере существует два квазиправильных паркета ( сферических многогранника ) — кубооктаэдр и икосододекаэдр .
На плоскости Лобачевского существует бесконечное множество квазиправильных паркетов вида где
Неоднородные паркеты
Существует бесконечное множество неоднородных ( англ. non-uniform ) паркетов, состоящих из правильных многоугольников.
- Неоднородные паркеты из правильных многоугольников
-
 3 2 .6 2 , 3 6
3 2 .6 2 , 3 6 -
 3 2 .6 2 , 3.6.3.6
3 2 .6 2 , 3.6.3.6 -
 3 2 .4.12, 3 6
3 2 .4.12, 3 6 -
 3.4 2 .6, 3.6.3.6
3.4 2 .6, 3.6.3.6
Периодические неоднородные паркеты можно классифицировать по числу орбит вершин, рёбер и граней. Если число орбит вершин равно n , паркет называется n -однородным ( англ. n-uniform ) или n -изогональным; если число орбит рёбер равно n — n -изотоксальным ( англ. n -isotoxal ). Вышеприведённые примеры представляют собой четыре из двадцати 2-однородных паркетов .
Непериодические паркеты и апериодические множества плиток



Разбиение T называется периодическим , если среди симметрий T существуют два параллельных переноса в непараллельных направлениях. В этом случае мозаику можно считать состоящей из повторений небольшого фрагмента, выложенного из элементов в узлах некоторой решётки. Множество прототипов (протомножество) P называется апериодическим , если оно реализуется в каких-то разбиениях плоскости, но ни одно из этих разбиений не является периодическим .
Первый пример апериодического множества плиток был найден в 1966 году и включал в себя 20 426 плиток Вана . Плитки Вана представляют собой квадраты одного размера с окрашенными сторонами; при построении мозаики разрешено совмещать плитки лишь одноцветными сторонами и запрещено переворачивать плитки.
Позднее были найдены апериодические протомножества с ме́ньшим числом плиток. Роджер Пенроуз обнаружил апериодические протомножества, состоящие из двух плиток .
В 2010 году Джошуа Соколар и Джон Тэйлор предложили апериодическое множество, состоящее из , которая представляет собой правильный шестиугольник с нанесённой разметкой в виде цветных линий и с дополнительными ограничениями, связанными с взаимным расположением не касающихся друг друга плиток . Существует модификация, не использующая подобных ограничений, но использующая несвязную плитку, т.е., плитку, не являющуюся . Существование единственной связной плитки без дополнительной разметки и ограничений, способной покрыть плоскость только апериодически, остаётся открытой проблемой .

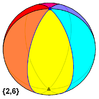
Сферические многогранники
Сферический паркет или сферический многогранник — разбиение сферы на дугами больших кругов .
Каждому из 5 платоновых тел соответствует правильный сферический паркет. Формально, пусть S — сфера с центром O , совпадающим с центром многогранника P . Проведённые из O лучи, проходящие через вершины многогранника P , пересекают сферу S в точках, являющихся вершинами соответствующего сферического паркета; рёбра многогранника P соответствуют дугам больших кругов на S .
Помимо сферических аналогов пяти «платоновых тел», существует два семейства правильных сферических многогранников, не имеющих эквивалентов среди многогранников с плоскими гранями: осоэдры — многогранники с двумя вершинами, находящимися на полюсах сферы, грани которых являются конгруэнтными двуугольниками , и диэдры — двойственные осоэдрам двугранники, вершины которых находятся на экваторе сферы.

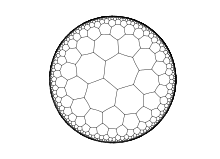
Гиперболические паркеты
Аксиома параллельности Евклида (точнее, одно из эквивалентных ей утверждений) гласит:
Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.
В геометрии Лобачевского, вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Для изображения гиперболической плоскости применяется одна из существующих моделей — модель Бельтрами — Клейна , конформный диск Пуанкаре , модель Пуанкаре на полуплоскости .
На евклидовой плоскости существует лишь три правильных паркета и 8 полуправильных. На гиперболической плоскости существует бесконечное множество даже правильных паркетов, включая паркеты с семью и более равносторонними треугольниками вокруг вершины, пятью и более квадратами, четырьмя и более правильными пятиугольниками (паркет с тремя пятиугольниками вокруг вершины является сферическим додекаэдром ), четырьмя и более правильными шестиугольниками и тремя и более равными правильными многоугольниками с количеством сторон более 6.
Задачи на паркетах
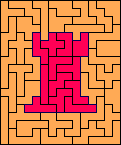
Большое количество задач и головоломок связано с разбиением прямоугольников (или других связных фигур) на плитки из определённого заданного множества протоплиток. Сами протоплитки при этом могут представлять собой связные объединения ячеек правильного паркета .
В частности, существует класс задач на замощение прямоугольников m × n плитками домино таким образом, чтобы в полученном разбиении не было прямой линии, пересекающей прямоугольник от края до края и не пересекающей ни одной плитки домино; такие прямоугольники называются «прочными» .
В других задачах устанавливается дополнительное ограничение на количество плиток каждого вида, используемых в замощении. В задачах, связанных с пентамино , требуется покрыть 12 фигурами заданное подмножество квадратного паркета, состоящее из 60 клеток (прямоугольники 3 × 20, 4 × 15, 5 × 12, 6 × 10, шахматная доска с вырезанным в центре квадратным тетрамино и др.); при этом каждая плитка должна быть использована ровно один раз .
Перечисление паркетов
Задача определения количества паркетов, состоящих из выпуклых многоугольников заданного типа, решена лишь частично:
- Любым треугольником или четырёхугольником можно замостить плоскость .
- Известно 15 пятиугольников, способных замостить плоскость; неизвестно, является ли этот перечень полным . Проблема перечисления пятиугольных паркетов имеет богатую историю , и, возможно, уже решена .
- Известно 3 типа шестиугольников, способных замостить плоскость .
- Невозможно замостить плоскость одинаковыми выпуклыми многоугольниками с числом сторон, большим или равным семи .
См. также
- Диаграмма Вороного
- Триангуляция Делоне
- Мозаика Пенроуза
- Проблема четырёх красок
- Стереографическая проекция
- Замощение (компьютерная графика)
Примечания
- ↑ Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- ↑ B. Grünbaum , G.C. Shephard. . — New York: W. H. Freeman & Co., 1987. — ISBN 0-7167-1193-1 .
- / Под ред. В. О. Бугаенко. — М. : МЦНМО , 2008. — С. 49. — 96 с. — ISBN 978-5-94057-331-9 . 9 августа 2013 года.
- ↑ . Математический цветник.
- . Encyclopedia of Mathematics. Дата обращения: 12 августа 2013. 2 сентября 2013 года.
- ↑ Кокстер, Введение в геометрию, 1966, §6, с. 100 — 104.
- ↑ Henry Martyn Cundy, A. P. Rollett. Mathematical Models (англ.) . — 2nd ed.. — Oxford University Press, 1961. — P. 59—65.
- Paul Bourke. . Дата обращения: 12 августа 2013. 2 сентября 2013 года.
- ↑ Chavey, D. (неопр.) // Computers and Mathematics with Applications . — 1989. — Т. 17 . — С. 147—165 . — doi : . 16 июня 2016 года.
- ↑ Math Forum. Дата обращения: 12 августа 2013. 2 сентября 2013 года.
- ↑ Голомб С.В. Полимино = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М. : Мир, 1975. — 207 с.
- ↑ Энциклопедия для детей. Т. 11. Математика / Глав. ред. М. Д. Аксёнова; метод. и отв. ред. В. А. Володин. — М. : Аванта+ , 2003. — С. 297—300. — 688 с. — ISBN 5-94623-072-7 .
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Steven Gillispie. . 26 октября 2008 года.
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- ↑ Steven Dutch. (2 июля 1999). 20 января 2013 года.
- ↑ John Baez. . Azimuth (5 февраля 2012). Дата обращения: 12 августа 2013. 2 сентября 2013 года.
- М. Веннинджер. Модели многогранников = Polyhedron Models / Перевод с английского В. В. Фирсова, под редакцией и с послесловием И. М. Яглома. — М. : Мир, 1974. — 236 с.
- George Hart. . Virtual Polyhedra: The Encyclopedia of Polyhedra. Дата обращения: 19 августа 2013. 2 сентября 2013 года.
- H. S. M. Coxeter. (англ.) . — 1973. — ISBN 0-486-61480-8 .
- Steven Dutch. (2 июля 1999). 20 января 2013 года.
-
Penrose R. (1979/80),
,
Math. Intell.
,
2
: 32—37
{{ citation }}: Проверьте значение даты:|year=( справка ) . Дата обращения: 18 августа 2013. Архивировано 7 июня 2011 года. (archived at) - ↑ David Austin. . Feature Column from the AMS. Дата обращения: 18 августа 2013. 2 сентября 2013 года.
- Burger, R. The Undecidability of the Domino Problem (англ.) // Memoirs of the American Mathematical Society. — 1966. — Vol. 66 . — P. 1—72 .
- . Tilings Encyclopedia. Дата обращения: 13 августа 2013. Архивировано из 2 сентября 2013 года.
- ↑ Socolar J. An Aperiodic Hexagonal Tile (неопр.) . — . — arXiv : .
- . Maxwell's Demon. Дата обращения: 18 августа 2013. 2 сентября 2013 года.
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Кокстер, Введение в геометрию, 1966, гл. 16, с. 415 — 440.
- ↑ Мартин Гарднер . Математические головоломки и развлечения = Mathematical Puzzles and Diversions / Пер. Ю. А. Данилова , под ред. Я. А. Смородинского . — 2-е. — М. : Мир, 1999. — ISBN 5-03-003340-8 .
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Michaël Rao . от 2 августа 2017 на Wayback Machine
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
Литература
- А. Н. Колмогоров . // Квант . — 1970. — № 3 .
- Ю. А. Шашкин. // МИФ. — 1998—99. — № 3 .
- О. Михайлов. // Квант . — 1979. — № 2 . 22 мая 2013 года.
- . Математический цветник. Сборник статей и задач = The Mathematical Gardner / Пер. с англ. Ю. А. Данилова ; под ред., с предисл. и прилож. И. М. Яглома . — М. : Мир, 1983. — С. 153—328. — 494 с.
- Г. С. М. Кокстер . Введение в геометрию = Introduction to geometry / Пер. с англ. А. Б. Катка и С. Б. Каток; под ред. Б. А. Розенфельда и И. М. Яглома. — М. : Наука, 1966. — 648 с.
- Grünbaum, Branko ; Shephard, G. C. Tilings and Patterns (неопр.) . — , 1987. — ISBN 0-7167-1193-1 .
Ссылки
- Хайдар Нурлигареев. . Элементы. 16 августа 2013 года.
- . Растрёпанный Блокнот. 4 ноября 2011 года.
- Влад Алексеев. . Невозможный мир. 8 августа 2013 года.
- Wolfram Alpha учащимся
- Jaap Scherphuis. . Jaap's Puzzle Page. Дата обращения: 15 августа 2013. 2 сентября 2013 года.
- Don Hatch. . — Изображения усечённых гиперболических паркетов. Дата обращения: 20 августа 2013. 2 сентября 2013 года.
- David E. Joyce. . — Java-апплет для отрисовки правильных и квазиправильных паркетов на гиперболической плоскости. Дата обращения: 23 августа 2013. 2 сентября 2013 года.
- Vladimir Bulatov. . Joint MAA/AMS meeting, New Orleans (7 января 2011). Дата обращения: 20 августа 2013. 2 сентября 2013 года.
- Demonolog. Применение векторной графики для изображения непериодических замощений.
- 2020-03-27
- 1







