«Звёзды» — гравюра на дереве, созданная нидерландским художником Маурицем Корнелисом Эшером в 1948 году, изображающая двух хамелеонов в многогранной клетке, плавающей в пространстве.

Хотя соединение трёх октаэдров , используемое для центральной клетки в «Звёздах», было изучено ранее в математике, оно, скорее всего, было придумано Эшером для этой работы без изучения этих исследований. Художник использовал подобные составные многогранные формы в нескольких других работах, включая «Кристалл» (1947), «Этюд для звёзд» (1948), «Двойной планетоид» (1949) и «Водопад» (1961).

На создание «Звёзд», вероятно, повлиял собственный интерес Эшера как к геометрии, так и к астрономии, а также долгая история использования геометрических форм для моделирования небес и стиля рисования, применявшегося Леонардо да Винчи . Критики интерпретировали сложную форму клетки как отсылку к двойным и тройным звёздам в астрономии или на двойные кристаллы в кристаллографии . В картине астрономический порядок со своими многогранными формами контрастирует с более хаотичными биологическими формами.

Эстампы «Звёзд» хранятся в постоянных коллекциях крупнейших музеев, включая Рейксмюсеум (Амстердам), Национальную галерею искусств (Вашингтон) и Национальную галерею Канады .

Описание

«Звёзды» представляют собой гравюру на дереве, созданную Эшером в октябре 1948 года . Хотя большинство опубликованных копий «Звёзд» являются монохромными , с белым рисунком на чёрном фоне, экземпляр в Национальной галерее Канады окрашен в различные оттенки бирюзового, жёлтого, зелёного и бледно-розового цветов .

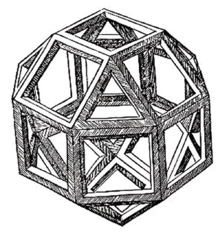
На гравюре доминирующем изображением является соединение трёх октаэдров (многогранников) , состоящее из трёх взаимосвязанных правильных октаэдров , плавающих в пространстве. Многочисленные другие многогранники и их соединения плавают на заднем плане; четыре самых больших из них: соединение куба и октаэдра в левом верхнем углу, звёздчатый октаэдр в правом верхнем углу, соединение двух кубов в левом нижнем углу и плотное соединение трёх октаэдров в правом нижнем углу. Меньшие многогранники, видимые в пределах гравюры, также включают в себя все пять правильных многогранников и ромбододекаэдр . Чтобы изобразить многогранники точно, Эшер делал их модели из картона .

Два хамелеона заключены в похожее на клетку по форме центральное соединение трёх октаэдров. Эшер писал, что они были выбраны в качестве его обитателей, потому что хамелеоны могут цепляться лапами и хвостами за прутья своей клетки, когда она вращается в пространстве . Хамелеон слева высовывает свой язык, возможно, что-то комментируя. Математик Гарольд Коксетер обращал внимание на его язык, отмечая его необычный спиралевидный конец .

Влияния

Интерес Эшера к геометрии был хорошо известен, но он также был заядлым астрономом-любителем, и в начале 1940-х годов стал членом голландской Ассоциации метеорологии и астрономии. У него был 6-сантиметровый рефрактор , и Эшер записывал результаты своих наблюдений за двойными звёздами .

Использование многогранников для моделирования небесных тел можно проследить до Платона , который в своём диалоге « Тимей » отождествлял правильный додекаэдр с формой небес, а его двенадцать граней с созвездиями зодиака . Позднее Иоганн Кеплер выдвинул теорию, что распределение расстояний планет от солнца можно объяснить формами пяти платоновых тел , вложенных друг в друга. Эшер взял модель этой системы вложенных многогранников и регулярно изображал её в своих работах, связанных с астрономией и другими мирами .

Эшер научился технике гравировки по дереву у Самуэля Йессуруна де Мескиты . В «Звёздах» он иллюстрировал восьмигранное соединение в виде срезанной каркасной модели , которая была использована Леонардо да Винчи в его иллюстрациях к книге Луки Пачоли 1509 года « О божественной пропорции » .

Звёздчатый октаэдр (или «восьмиконечная звезда» ( лат. stella octangula )), расположенный в правом верхнем углу «Звёзд», был впервые описан Пачоли, а позднее вновь открыт Кеплером, который дал ему своё астрономическое название . Математик Гарольд Коксетер отмечал, что форма центральной клетки с хамелеонами в звёздах ранее была описана в 1900 году геометром , чья книга «Vielecke und Vielflache» содержала фотографию модели той же формы. Однако Эшер не знал об этом источнике, и Коксетер писал: «замечательно, что Эшер, не зная алгебры или аналитической геометрии, смог заново открыть эту очень симметричную фигуру .»

Анализ

Мартин Бич интерпретирует многогранные соединения в «Звёздах» как соответствия системам двойных и тройных звёзд в астрономии . Он писал, что для Эшера математическая упорядоченность многогранников отображает «стабильность и вневременное качество» небес, и точно так же Марианна Л. Тойбер отмечала, что «Звёзды» «воспевают идентификацию Эшера с неоплатонической верой Иоганна Кеплера в лежащий в основе Вселенной математический порядок .»

С другой стороны, Говард У. Яффе интерпретировал многогранные формы в «Звездах» с позиций кристаллографии , как «блестяще огранённые драгоценные камни», плавающие в пространстве, с его составными многогранниками, представляющими их кристаллических двойников . Однако Р. А. Данлэп указывал на контраст между порядком многогранных форм и более хаотичной биологической природой заключённых в них хамелеонов . В том же духе Бич замечал, что сами звёзды передают напряжение между порядком и хаосом: несмотря на их симметричные формы, звёзды разбросаны, по-видимому, случайным образом и изменяются бессистемно друг от друга. Как писал сам Эшер о центральной клетке с хамелеонами: «я не удивлюсь, если она немного покачнётся .»

Связанные работы

Тесно связана со «Звёздами» другая гравюра на дереве Эшера «Этюд для звёзд», завершённая в августе 1948 года . На ней изображены каркасные версии нескольких одинаковых многогранников и многогранных соединений, плавающих в чёрном цвете внутри квадратной композиции, но без хамелеонов. Самый большой многогранник, показанный в «Этюде для звёзд», , также является одним из двух многогранников, чётко изображённых в литографии Эшера 1961 года « Водопад » .

Звёздчатый октаэдр , соединение двух тетраэдров, которое изображено в правом верхнем углу «Звёзд», также образует центральную форму в другой астрономической работе Эшера «Двойной планетоид» (1949) . Соединение куба и октаэдра в верхнем левом углу «Звёзд» было использовано ранее Эшером в «Кристалле» (1947) .

В своей более поздней работе «Четыре правильных твёрдых тела (Стереометрическая фигура)» Эшер вернулся к теме многогранных соединений, изобразив более приближённую к кеплеровской форму, в которой соединение куба и октаэдра вложено в соединение додекаэдра и икосаэдра .

Коллекции и публикации

«Звёзды» использовались в качестве обложки для антологии 1962 года «Best Fantasy Stories», изданных под редакцией Брайана Олдисса , и для итальянского издания оккультного путеводителя « Утро магов » 1971 года . Работа Эшера также была изображена на фронтисписе учебника 1996 года по кристаллографии .

Помимо Музея Эшера эстампы «Звёзд» находятся в постоянных коллекциях Рейксмюсеума (Амстердам) , Национальной галереи искусств (Вашингтон) , Национальной галереи Канады , и Бостонской публичной библиотеки .

Примечания