${\displaystyle y}$

${\displaystyle O}$

${\displaystyle {\mathit {1}}}$

${\displaystyle A}$

${\displaystyle {\mathit {2}}}$

${\displaystyle B}$

${\displaystyle {\mathit {3}}}$

${\displaystyle C}$

${\displaystyle x}$

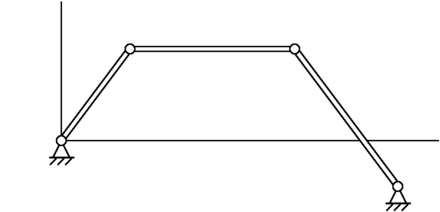
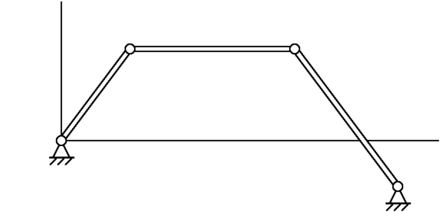
Шарни́рный четырёхзве́нник — плоский механизм из четырёх звеньев, соединенных между собой вращательными кинематическими парами . Одно из этих звеньев в теории механизмов и машин принимают за стойку , т. е. неподвижное звено (хотя, например, для механизмов транспортных машин понятие неподвижности стойки оказывается условностью, поскольку в этом случае сама стойка движется) .

Для звеньев плоских механизмов в теории механизмов и машин используют следующую терминологию:

• кривошип — звено плоского механизма, которое образует вращательную пару со стойкой и может совершать вокруг оси пары полный оборот ;
• коромысло — звено плоского механизма, которое образует вращательную пару со стойкой, но не может совершать полный оборот вокруг оси пары;
• шатун — звено плоского механизма, связанное вращательными парами с подвижными его звеньями, но не со стойкой.

Для шарнирного четырёхзвенника справедлива доказанная немецким механиком Ф. Грасгофом теорема Грасгофа о шарнирном четырёхзвеннике (иногда её также называют правилом Грасгофа ): «Наименьшее звено является кривошипом, если сумма длин наименьшего и любого другого звена меньше суммы длин остальных двух звеньев (под «наименьшим» понимается звено минимальной длины).

Разновидности шарнирных четырёхзвенников

Применяя правило Грасгофа, удаётся подразделить все шарнирные четырёхзвенники на 3 группы:

• механизм будет кривошипно-коромысловым , если длины его звеньев удовлетворяют правилу Грасгофа и за стойку принято звено, соседнее с наименьшим;
• механизм будет двухкривошипным , если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев, и за стойку принято самое короткое звено;
• механизм будет двухкоромысловым , если либо правило Грасгофа не выполнено, либо оно выполнено, но самое короткое звено не соединено со стойкой (т. е. оно является шатуном и потому не может быть кривошипом).

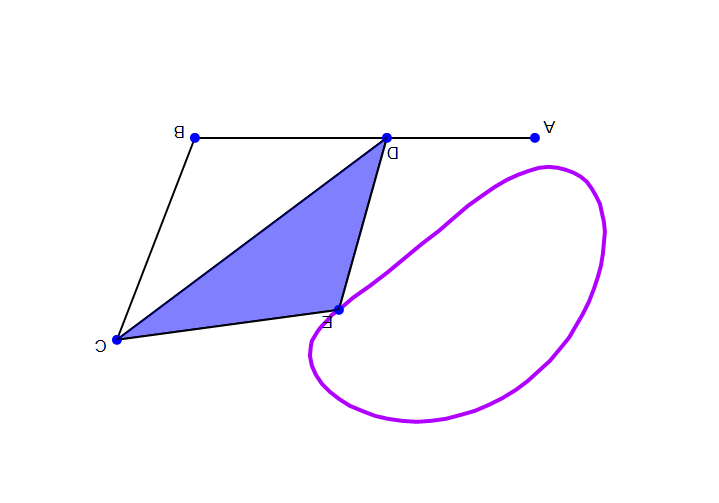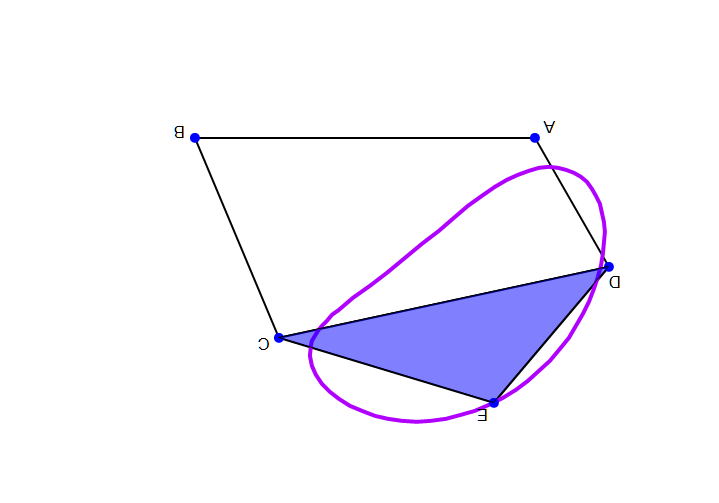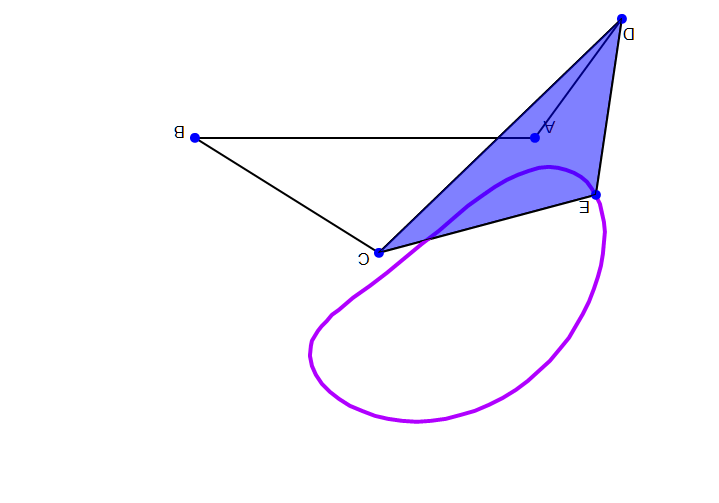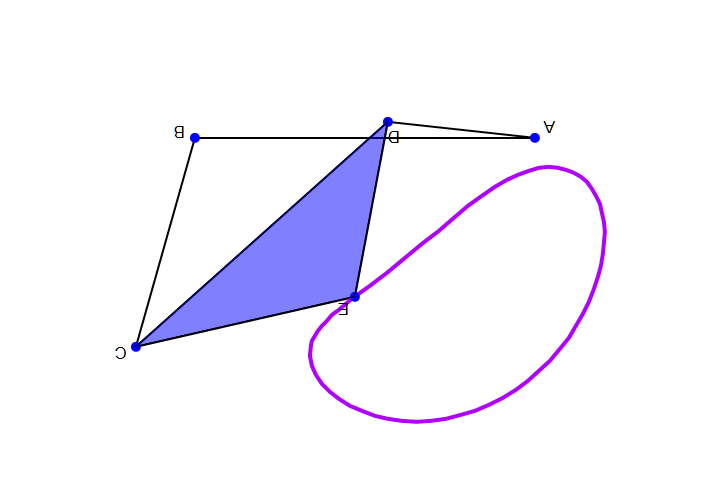
Так, представленный на приведённом выше рисунке шарнирный четырёхзвенник представляет собой двухкоромысловый механизм, поскольку правило Грасгофа для него не выполняется.

Справа дано анимированное изображение кривошипно-коромыслового механизма  (здесь стойкой служит звено ${\displaystyle AB}$ ,  кривошипом — звено ${\displaystyle AD}$ ,  коромыслом — звено ${\displaystyle BC}$ и шатуном — треугольник ${\displaystyle DCE}$ ).

Кинематический анализ

Кинематический анализ шарнирного четырёхзвенника можно выполнить, применяя методы, основанные на построении плана скоростей . Можно воспользоваться и аналитическими методами — как общего характера (например, ), так и методами, специально предназначенными для кинематического анализа шарнирного четырёхзвенника.

К числу последних относится предложенный в 2002 г. М. Н. Кирсановым метод, основанный на составлении уравнений трёх угловых скоростей . Составим такие уравнения для механизма, представленного на верхнем рисунке.

Для этого присвоим шарнирам ${\displaystyle O,\,A,\,B,\,C}$ номера ${\displaystyle {\mathit {1}},\,{\mathit {2}},\,{\mathit {3}},\,{\mathit {4}}}$ ;  при этом для декартовых координат шарнира ${\displaystyle O}$ получаем обозначения ${\displaystyle x_{1}}$ и ${\displaystyle y_{1}}$ ,  и т. п.

Уравнения трёх угловых скоростей для рассматриваемого шарнирного четырёхзвенника имеют вид

${\displaystyle {\omega }_{1z}\,(x_{2}\,-\,x_{1})\,+\,{\omega }_{2z}\,(x_{3}\,-\,x_{2})\,+\,{\omega }_{3z}\,(x_{4}\,-\,x_{3})\,\;=\;\,0}$ ,

${\displaystyle {\omega }_{1z}\,(y_{2}\,-\,y_{1})\,\,+\,{\omega }_{2z}\,(y_{3}\,-\,y_{2})\,\,+\,{\omega }_{3z}\,(y_{4}\,-\,y_{3})\,\;=\;\,0}$ ,

где ${\displaystyle {\omega }_{1z},\,{\omega }_{2z},\,{\omega }_{3z}}$ — угловые скорости звеньев ${\displaystyle {\mathit {1}},\,{\mathit {2}},\,{\mathit {3}}}$ .

Пользуясь данными уравнениями, можно, например, найти для текущей конфигурации механизма значения угловых скоростей двух его звеньев, если значение угловой скорости третьего подвижного звена известно.

Применение

Примеры практического применения шарнирного четырёхзвенника — механизм насоса, механизм сеноворошилки, механизм тестомесильной машины, механизм подъёмного крана. К шарнирным четырёхзвенникам относятся и четырёхзвенные приближённо-направляющие механизмы , предложенные П. Л. Чебышёвым (в них обеспечивается приближённое прямолинейное движение одной из точек шатуна). Частным случаем шарнирного четырёхзвенника является механизм шарнирного параллелограмма — четырёхзвенника с попарно равными по длине и попарно параллельными сторонами .

Примечания

Литература

• Артоболевский И. И. Теория механизмов. — М. : Наука , 1965. — 776 с.
• Фролов К. В. , Попов С. А., Мусатов А. К. Теория механизмов и машин / Под ред. К. В. Фролова. — М. : Высшая школа , 1987. — 496 с.
• Юдин В. А., Петрокас Л. В. Теория механизмов и машин. — М. : Высшая школа , 1967. — 528 с.