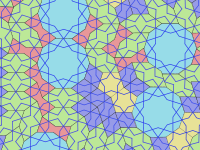
Мозаики «гирих» — это набор пяти плиток , использовавшихся для создания для украшения зданий в исламской архитектуре . Плитки использовались примерно с 12-го века и орнаменты существенно улучшились к моменту построения усыпальницы в городе Исфахан в Иране (построена в 1453).

Пять плиток мозаики включают:

• правильный десятиугольник с внутренними углами 144°;
• удлиненный (неправильный выпуклый) шестиугольник с внутренними углами 72°, 144°, 144°, 72°, 144°, 144°;
• галстук-бабочка (невыпуклый шестиугольник) с внутренними углами 72°, 72°, 216°, 72°, 72°, 216°;
• ромб с внутренними углами 72°, 108°, 72°, 108°;
• правильный пятиугольник с внутренними углами 108°.

Все рёбра этих плиток имеют одну и ту же длину, а все углы кратны 36° (π/5 радиан ). Четыре плитки (кроме пятиугольника) имеют двустороннюю (зеркальную) симметрию относительно двух перпендикулярных осей. Некоторые плитки имеют дополнительные симметрии. В частности, десятиугольник имеет десятикратную вращательную симметрию (вращение на 36°), а пятиугольник имеет пятикратную вращательную симметрию (вращение на 72°).

Собственно, гирих — это линии ( ), которым декорированы плитки. Плитки использовались для создания орнамента (гириха). На языке фарси слово означает "узел" . В большинстве случаев виден только гирих, (и другие украшения в виде цветов), но не границы самих плиток. Гирих является ломаными отрезками, пересекающими границы плиток по центру под углом 54° (3π/10) к ребру. Две перекрещивающиеся линии гириха пересекают каждое ребро плитки. Большинство плиток имеют единственный орнамент внутри, соответствующий симметрии плитки. Однако десятиугольник имеет два возможных орнамента гириха, один из которых имеет только пятикратную, а не десятикратную симметрию.

Математика плиток «гирих»

В 2007 году физики и Пол Стейнхардт высказали предположение, что мозаика «гирих» обладает свойствами, сопоставимыми со свойствами самоподобных фрактальных квазикристаллических мозаик, таких как мозаики Пенроуза , но возраст гириха насчитывает пять столетий .

Это открытие было подтверждено как анализом существующих орнаментов, так и изучением персидских свитков 15-го столетия. Однако у нас нет никаких намёков, знали ли архитекторы что-нибудь о вовлечённой математике. В основном, есть мнение, что такие узоры создавались путём рисования зигзагообразных контуров с помощью линейки и циркуля. Можно исследовать узоры, найденные в свитках, таких как , длиной в 29.5 метров. Найденный во дворце Топкапы в Стамбуле, административном центре Османской империи и датированной, как полагают, концом 15-го столетия, свиток даёт последовательность двухмерных и трёхмерных геометрических узоров. На свитке нет текста, но имеется сетка и обозначенные цветом симметрии и различные трёхмерные проекции. Рисунки в свитке могли служить образцами орнаментов для художников, изготовлявших плитки, а формы плиток гириха определяли, каким образом они могли быть скомбинированы для получения орнамента. Таким путём рабочие могли делать крайне сложные орнаменты без вовлечения математики и без понимания лежащих в основе принципов .

Создание повторяющихся орнаментов из ограниченного числа геометрических фигур, доступных рабочим того времени, похоже на практику более современных готических европейских мастеров. Художники обоих стилей, основываясь на имеющихся геометрических фигурах, сосредотачивались на создании максимально отличающихся орнаментов. Это требовало совсем другой квалификации и опыта, чем у математиков .

Примеры

• Примеры орнаментов
• 
  Сложные гирих-орнаменты с 16-, 10- и 8-угольными звёздами в различном масштабе на потолке в Ширазе , 1935
• 
  Окно в апартаментах кронпринца во дворце Топкапы , Стамбул , Турция, с 6-угольными звёздами. Окружение звезды имеет вид цветка.
• 
  Внутренний вид арки в Зелёной мечети в Бурсе , Турция (1424), с 10-угольными звёздами и пятиугольниками

См. также

• Апериодичная мозаика
• Мозаика Пенроуза
• Зулляйдж

Примечания

Литература

• Sebastian R. Prange. The Tiles of Infinity // Saudi Aramco World. — 2009.
• Peter J. Lu, Paul J. Steinhardt. Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture // Science . — 2007. — Т. 315 , вып. 5815 . — doi : . — Bibcode : . — . 7 октября 2009 года.
• Gulru Necipoglu. The Topkapi Scroll: Geometry and Ornament in Islamic Architecture. — Santa Monic: Getty Research Institute, 1995. — ISBN 13: 978-0892363353, 10: 0892363355.

Ссылки

• от 19 ноября 2014 на Wayback Machine
• от 29 ноября 2020 на Wayback Machine
• от 3 января 2012 на Wayback Machine
• (неопр.) . Harvard University Gazette (22 февраля 2007). Дата обращения: 14 марта 2007. 11 мая 2015 года.
• (неопр.) . New Scientist (22 февраля 2007). Дата обращения: 14 марта 2007. 31 мая 2015 года.