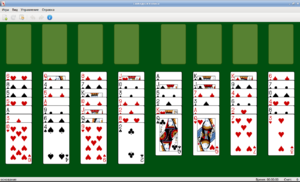
« Свободная ячейка » ( англ. FreeCell ) — карточный пасьянс . Поскольку пасьянс относительно новый и известен исключительно по компьютерным реализациям, устоявшегося русского названия нет. В Windows XP игра некорректно названа « Солите́р » (этот пасьянс отличается от «Свободной ячейки» одним правилом) .

Пасьянс удачно сочетает высокую сложность (намного сложнее « Косынки »), совершенную информацию ( полную + отсутствие дальнейшей случайности) и мизерный процент комбинаций, которые невозможно сложить.

Правила

• Используется стандартная колода карт (52 карты).
• Раскладывается вся колода в 8 колонок, лицом вверх. Таким образом, будет четыре колонки по 7 карт и ещё четыре — по 6.
• Также есть 4 ячейки, именуемых «домом», и 4 «свободных» ячейки. В начале игры все они пусты.
• Разрешено перекладывать одну карту из колонки или свободной ячейки:
  • в любую другую колонку — на следующую по старшинству карту другого цвета (например, чёрного валета — только на красную даму).
  • либо на свободную ячейку, если она пуста (таким образом, каждая из свободных ячеек может хранить только одну карту);
  • либо в пустую колонку — без ограничений;
  • либо в «дом» — карты одной масти, начиная с туза и заканчивая королём.
• Пасьянс сходится, если удаётся переместить всю колоду в «дом».

Если нужно перенести стопку карт, это можно сделать только по одной, используя пустые колонки и свободные ячейки. Имея n свободных ячеек и m пустых колонок, можно перенести в другое место ${\displaystyle (n+1)\cdot 2^{m}}$ сложенных по порядку карт , такие комбинации называются «суперходы» ( англ. supermoves ). Компьютерные версии обычно показывают суперход во всех деталях; играющие с настоящей колодой просто переносят стопку, убедившись, что карты действительно сложены по порядку, а пустых ячеек достаточно. Иногда можно перенести ещё больше карт, придержав какую-то часть в занятой колонке, но это уже комбинация суперходов .

Варианты правил

Марсель

Используется одна колода в 52 карты, как и в стандартных правилах.

Карты раскладываются картинкой вверх в 7 столбцов по 7 карт. Оставшиеся три карты кладутся в низ любых столбцов (одного или нескольких) по выбору раскладывающего.

Свободных ячеек можно использовать только три (а не четыре, как в стандартных правилах).

Упорядоченную серию карт (в нисходящем порядке, с чередованием цветов) можно перемещать целиком, независимо от количества свободных ячеек и пустых столбцов.

Цель игры та же, что в стандартных правилах: собрать карты в масть на тузах в базовом ряду.

Солитер

Игра отличается от «Свободной ячейки» одним правилом: карты в колонках выкладываются по масти, по одной за ход. Например, В♡ — только на Д♡ .

Солитер намного сложнее «Свободной ячейки», высок процент неразрешимых комбинаций, поэтому есть и упрощённые варианты.

Но иногда Солитером называют классическую версию «Свободной ячейки».

Солитер 6×6

Вариант пасьянса для колоды в 36 карт.

Колода раскладывается в 6 столбцов по 6 карт. Используются три свободных ячейки. Правила аналогичны стандартным для «Солитера»: карты в столбцах можно перекладывать в нисходящем порядке по масти, по одной за ход (например, трефовую десятку можно положить на трефового валета). Цель пасьянса — собрать карты на базовые тузы в восходящем порядке (6, 7, 8, 9, 10, В, Д, К). Существует вариант со сбором карт на базовые в нисходящем порядке (К, Д, В, 10, 9, 8, 7, 6).

Солитер с одной и двумя мастями

В этом варианте пасьянса используется половина стандартной колоды в 52 карты . Из неё выбирают какие-нибудь две масти (26 карт). Их раскладывают в 6 столбцов: четыре столбца по 4 карты и два по 5 карт.

Используются две свободные ячейки. В базовом ряду, естественно, есть только два места для тузов.

Перекладывать карты между столбцами можно по масти в нисходящем порядке, по одной. В базовый ряд собираются карты по масти в восходящем порядке.

Существует также вариант пасьянса с одной мастью (13 карт). Их раскладывают в 5 столбцов (три по 3 карты и два по 2 карты). Используется одна свободная ячейка и одно базовое место для единственного туза.

Этот вариант пасьянса при правильной игре сходится всегда. Один из наиболее трудных раскладов — упорядоченная в восходящем порядке колода (1-й горизонтальный ряд — Т, 2, 3, 4, 5; 2-й — 6, 7, 8, 9, 10; 3-й — В, Д, К). Эта задача решается за 23 хода .

История

Предтечами «Свободной ячейки» можно считать пасьянсы «Восьмёрка» и «Сорок разбойников» (он же «Наполеон на острове святой Елены») . В 1968 году М. Гарднер опубликовал пасьянс под авторством некоего Бейкера, однако в нём карты складывались по масти. Журнал « Наука и жизнь » мгновенно перепечатал пасьянс, окрестив его «Солитером», периодически предлагал решить головоломные расклады.

Изобретатель «Свободной ячейки» Пол Олфилл ( Paul Alfille ), будучи ещё ребёнком, жаловался, что большинство пасьянсов оставляли колоду отсортированной по масти; чтобы начать новую игру, требовалось долгая и тщательная перетасовка . Установив правило «чёрный-красный», Олфилл улучшил состояние колоды: даже если пасьянс решён, позиция становится очевидной задолго до того, как будут сложены все карты, и часть колоды складывается по масти, а часть — поочерёдно . Игра оказалась довольно сложной, но неразрешимые комбинации практически не выпадали.

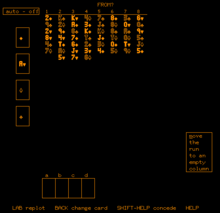
Впоследствии, в 1978 году , Олфилл реализовал свою игру в рамках системы программированного обучения PLATO на языке программирования . Благодаря высокому (по тем временам) разрешению PLATO — 512×512 — удалось нарисовать разборчивые изображения мастей, несмотря на монохромный монитор.

В дальнейшем Джим Хорн ( Jim Horne ) реализовал «Свободную ячейку» для DOS (в текстовом виде), в 1992 — для Windows . Неизвестно, где Хорн узнал о «Свободной ячейке» — вероятно, будучи студентом, имел дело с PLATO. Компания Microsoft включила игру в пакет , позднее — в Win32s . Впрочем, «Свободная ячейка» оставалась малоизвестной, пока не оказалась в стандартной поставке Windows 95 . В дальнейшем игру включали во все версии Windows вплоть до Windows 7 . Из Windows 8 игру выбросили; она (вместе с четырьмя другими пасьянсами) доступна из магазина программ.

Только после появления Microsoft FreeCell изобретение Олфилла стали включать в книги о карточных играх.

Реализации

Microsoft

Реализация Джима Хорна, опубликованная под именем Microsoft FreeCell , считается классической. Сторонние разработчики обычно делают в своих программах генератор раскладов, совместимый с нумерацией Microsoft .

Теоретическое количество раскладов в пасьянсе — 52! или 8,06·10 ⁶⁷ . Если расклады с переставленными колонками и переименованными мастями считать одинаковыми, то число раскладов будет равно 1,75·10 ⁶⁴ . В MS FreeCell представлено лишь 32000 раскладов, генерирующихся 15-битным генератором псевдослучайных чисел ; встроенная справка заявляла:

В общем случае это неверно: в качестве « пасхального яйца » в игре можно задать явно неразрешимые расклады −1 и −2. Чтобы проверить 32000 раскладов Microsoft, в интернете появился краудсорсинг -проект, проверяющий, действительно ли все расклады разрешимы. В проекте были задействованы более чем 100 заядлых картёжников; к 1995 году только расклад № 11982 не поддался ни одному участнику. Несмотря на то, что задача NP-полна по количеству карт , к середине 2000-х годов удалось реализовать достаточно быстрый полный перебор и показать, что для этого расклада решения действительно нет.

В Windows XP количество раскладов увеличено до 1 миллиона, первые 32000 раскладов были теми же. Помимо расклада 11982, решение не существует для раскладов 146692, 186216, 455889, 495505, 512118, 517776 и 781948.

В версии Microsoft суперходы реализованы, но не полностью: если колонок больше одной или нет свободных ячеек, программа может и не заметить суперход . Например, имея одну пустую ячейку и две колонки, можно перенести восемь карт; MS FreeCell перенесёт только четыре.

Существует способ быстрого выигрыша: нажимаем одновременно клавиши ⇧ Shift + Ctrl + F10 , в полученном окне выбираем: «Прервать» — выиграть, «Повтор» — проиграть, «Пропустить» — отмена.

Другие виды

• Aisleriot — набор пасьянсов.
• — набор пасьянсов в составе KDE Games .

Вероятность победы

По современным данным, вероятность выпадения разрешимой комбинации оценивается более чем в 99,99 % — одна неразрешимая комбинация на 78 000 разрешимых. Без свободных ячеек сходится всего 0,2 % раскладов. Чтобы любой расклад гарантированно сошёлся, нужно не менее семи свободных ячеек.

Если упростить правила и разрешить перемещать упорядоченную стопку целиком, не используя свободных ячеек, разрешимы все 1 млн раскладов Microsoft — но потенциально неразрешимые также остались. Поскольку шансы на плохой расклад и без этого крайне малы, такое упрощение считается сомнительным.

См. также

• Microsoft Solitaire
• Косынка
• Паук

Примечания