Точка Немо
- 1 year ago
- 0
- 0
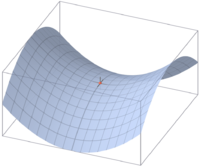

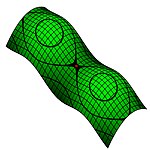
Седловая точка в математическом анализе — такая точка из области определения функции , которая является стационарной для данной функции , однако не является её локальным экстремумом . Является точкой равновесия в . В такой точке, если рассматривается функция двух переменных, образованная графиком функции поверхность обычно напоминает по форме седло или горный перевал — выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний . Например, два холма, между которыми находится высокий перевал , образуют седловую точку в вершине этого перевала : на карте высот это будет выглядеть как центр «восьмерки», образованной соответствующими изолиниями .
Проверить, является ли данная стационарная точка функции F ( x , y ) двух переменных седловой, можно, вычислив матрицу Гессе функции в этой точке: если гессиан будет неопределенной квадратичной формой , то данная точка — седловая. Например, составив матрицу Гессе функции в стационарной точке получим матрицу:
которая является неопределенной. Поэтому, точка данной функции — седловая. Однако вышеприведенный критерий предоставляет только достаточное условие наличия седловой точки. Например, является седловой точкой функции , но матрица Гессе в данном случае будет нулевой матрицей, которую, по определению, нельзя назвать неопределенной.
В общем случае, седловой точкой гладкой функции ( график которой изображает кривую , поверхность или гиперповерхность ) называется такая стационарная точка, в окрестности которой данная кривая/поверхность/гиперповерхность не лежит полностью по одну сторону касательного пространства в данной точке.
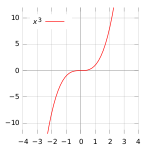
В случае функции одной переменной, седловая точка — такая точка, которая одновременно является и стационарной точкой, и точкой перегиба (точка перегиба не является локальным экстремумом ).