Interested Article - Карта Рамачандрана

elizabeth
  • 2021-07-06
  • 2

Оригинальные регионы φ,ψ , уменьшенного радиуса с ослабленным углом тау от Рамачандрана с обновленными метками и осями.
Основные двугранные углы φ и ψ (и ω). Все три угла составляют 180° в показанной конфигурации.

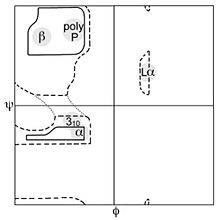
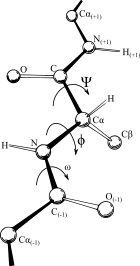
В биохимии карта Рамачандрана (также известная как график Рама , диаграмма Рамачандрана или график [φ,ψ] ), первоначально разработанная в 1963 году , К. Рамакришнаном и , представляет собой способ визуализирования энергетически разрешенных областей для двугранных углов ψ основной цепи в зависимости от φ аминокислотных остатков в структуре белка . Рисунок слева иллюстрирует определение основных двугранных углов φ и ψ (названных Рамачандраном φ и φ'). Угол ω при пептидной связи обычно составляет 180°, поскольку характер частичной двойной связи сохраняет пептидную связь плоской . На рисунке вверху справа показаны разрешенные конформационные области φ,ψ основной цепи из публикации Ramachandran et al. Расчеты 1963 и 1968 годов: полный радиус обозначен сплошным контуром, уменьшенный радиус — пунктиром, а ослабленный угол тау (N-Cα-C) — пунктирными линиями . Поскольку значения двугранного угла являются круглыми, а 0° соответствует 360°, края графика Рамачандрана «заворачиваются» справа налево и снизу вверх. Например, небольшая полоска разрешенных значений вдоль нижнего левого края графика является продолжением большой области расширенной цепочки в левом верхнем углу.

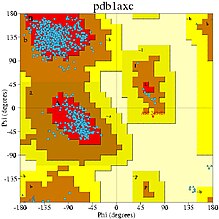
Карта Рамачандрана, полученная на основе человека, тримерного белка -зажима ДНК , который содержит как β-лист , так и α-спираль ( PDB ID 1AXC). Красная, коричневая и жёлтая области обозначают предпочтительные, разрешенные и «щедро разрешенные» области, определённые с помощью ProCheck.

Использование

Карту Рамачандрана можно использовать двумя различными способами. Один из них — теоретически показать, какие значения или конформации углов ψ и φ возможны для аминокислотного остатка в белке (как показано вверху справа). Во-вторых, с помощью карты можно показать эмпирическое распределение точек данных, наблюдаемых в одной структуре (как здесь справа) при использовании для или в базе данных, состоящей из многих структур (как на трех нижних графиках слева). Любой случай обычно отображается на фоне теоретически предпочтительных регионов.

Аминокислотные предпочтения

Можно было бы ожидать, что более крупные боковые цепи приведут к большему количеству ограничений и, следовательно, к меньшей допустимой области на графике Рамачандрана, но эффект боковых цепей невелик . На практике основным наблюдаемым эффектом является наличие или отсутствие метиленовой группы у Cβ . Глицин имеет только атом водорода в боковой цепи с гораздо меньшим радиусом Ван-дер-Ваальса , чем группы CH 3 , CH 2 или CH, которые начинают боковую цепь всех других аминокислот. Следовательно, он наименее ограничен, и это видно на графике Рамачандрана для глицина (см. График Gly в ), для которого допустимая область значительно больше. Напротив, график Рамачандрана для пролина с его 5-членной кольцевой боковой цепью, соединяющей Cα с основной цепью N, показывает ограниченное количество возможных комбинаций ψ и φ (см. график Pro в ). Остаток, предшествующий пролину («препролин»), также имеет ограниченные комбинации по сравнению с общим случаем.

Более свежие обновления

Первый график Рамачандрана был рассчитан сразу после того, как была определена первая структура белка с атомным разрешением ( миоглобин , в 1960 году ), хотя выводы были основаны на низкомолекулярной кристаллографии коротких пептидов. Теперь, много десятилетий спустя, существуют десятки тысяч белковых структур высокого разрешения, определённых с помощью рентгеновской кристаллографии и депонированных в Банке данных белков (PDB) . Многие исследования использовали эти данные для создания более подробных и точных графиков φ,ψ (например, Morris et al. 1992 ; Kleywegt & Jones 1996 ; Hooft et al. 1997 ; Hovmöller et al. 2002 ; Lovell et al. 2003 ; Anderson et al. 2005. ; Ting et al. 2010 ) .

Четыре фигуры ниже показывают данные из большого набора высокоразрешительных структур и контур для предпочтительных и разрешенных конформационных областей для общего случая (все аминокислоты, кроме Gly, Pro и pre-Pro), для Gly и для Pro. Наиболее распространенные области маркируются: α для α-геликси, Lα для леворучной геликси, β для β-лист и ppII для полипролина II. Такой кластер описывается альтернативно в системе ABEGO, где каждая буква представляет собой α (и 3 10 ) спираль, правые β-листы (и расширенные структуры), левые спиральники, левые листы и, наконец, неразрывные пептидные цис-связи, которые иногда встречаются с пролином; он использовался при классификации мотивов и в последнее время для проектирования белков.

Хотя график Рамачандрана был учебным пособием для объяснения структурного поведения пептидной связи, исчерпывающее исследование того, как пептид ведет себя в каждой области графика Рамачандрана, было опубликовано лишь недавно (Mannige 2017 ).

Отделение молекулярной биофизики Индийского института науки отметило 50-летие карты Рамачандрана , организовав Международную конференцию по биомолекулярным формам и функциям 8-11 января 2013 года .

Связанные соглашения

Можно также построить двугранные углы в полисахаридах (например, с помощью ) .

Галерея

  • Карта Рамачандрана для общего случая; данные из Lovell 2003
    Карта Рамачандрана для общего случая; данные из Lovell 2003
  • Карта Рамачандрана для глицина
    Карта Рамачандрана для глицина
  • Карта Рамачандрана для пролина
    Карта Рамачандрана для пролина
  • Карта Рамачандрана для предпролина
    Карта Рамачандрана для предпролина

Программное обеспечение

  • (Structure Analysis and Verification) — использует WHATCHECK, PROCHECK и составляет свою собственную внутреннюю карту Рамачандрана
  • STING
  • Pymol с расширением DynoPlot
  • VMD, распространяется с помощью плагина dynamic Ramachandran plot plugin
  • , автономные процедуры проверки из программного обеспечения WHAT IF
  • UCSF Chimera
  • Sirius
  • — в меню «Инструменты» находятся высококачественные графики с региональными контурами
  • Список аналогичного программного обеспечения смотрите также в PDB

Рекомендации

  1. Ramachandran, G.N. (1963). "Stereochemistry of polypeptide chain configurations". Journal of Molecular Biology . 7 : 95—9. doi : . PMID .
  2. Richardson, J.S. The Anatomy and Taxonomy of Protein Structure // Anatomy and Taxonomy of Protein Structures. — 1981. — Vol. 34. — P. 167–339. — ISBN 9780120342341 . — doi : .
  3. Pauling, L. (1951). "The Structure of Proteins: Two Hydrogen-Bonded Helical Configurations of the Polypeptide Chain". Proceedings of the National Academy of Sciences of the United States of America . 37 (4): 205—211. Bibcode : . doi : . PMID .
  4. Ramachandran, G.N. Conformation of polypeptides and proteins / G.N. Ramachandran, V. Sasiskharan. — 1968. — Vol. 23. — P. 283–437. — ISBN 9780120342235 . — doi : .
  5. ↑ Chakrabarti, Pinak (2001). "The interrelationships of side-chain and main-chain conformations in proteins". Progress in Biophysics and Molecular Biology . 76 (1—2): 1—102. doi : . PMID .
  6. Kendrew, J.C. (1960). "Structure of myoglobin: a three-dimensional Fourier synthesis at 2Å resolution". Nature . 185 (4711): 422—427. Bibcode : . doi : . PMID .
  7. Morris, A.L. (1992). "Stereochemical quality of protein structure coordinates". Proteins: Structure, Function, and Genetics . 12 (4): 345—64. doi : . PMID .
  8. Kleywegt, G.J. (1996). "Phi/psi-chology: Ramachandran revisited". Structure . 4 (12): 1395—400. doi : . PMID .
  9. Hooft, R.W.W. (1997). "Objectively judging the quality of a protein structure from a Ramachandran plot". Comput Appl Biosci . 13 (4): 425—430. doi : . PMID .
  10. Hovmöller, S. (2002). . Acta Crystallographica D . 58 (Pt 5): 768—76. doi : . PMID .
  11. Simon C. Lovell, Ian W. Davis, W. Bryan Arendall, Paul I. W. de Bakker, J. Michael Word, Michael G. Prisant, Jane S. Richardson, David C. Richardson. (англ.) // Proteins: Structure, Function, and Bioinformatics. — 2003-02-15. — Vol. 50 , iss. 3 . — P. 437–450 . — ISSN . — doi : .
  12. "Main-chain conformational tendencies of amino acids". Proteins . 60 (4): 679—89. 2005. doi : . PMID .
  13. Ting, D. (2010). "Neighbor-dependent Ramachandran probability distributions of amino acids developed from a hierarchical Dirichlet process model". PLOS Computational Biology . 6 (4): e1000763. Bibcode : . doi : . PMID . {{ cite journal }} : Википедия:Обслуживание CS1 (не помеченный открытым DOI) ( ссылка )
  14. Lovell, S.C. (2003). "Structure validation by Cα geometry: ϕ,ψ and Cβ deviation". Proteins: Structure, Function, and Genetics . 50 (3): 437—50. doi : . PMID .
  15. Wintjens, René T. (January 1996). "Automatic Classification and Analysis of αα-Turn Motifs in Proteins". Journal of Molecular Biology . 255 (1): 235—253. doi : . PMID .
  16. Lin, Yu-Ru (6 October 2015). "Control over overall shape and size in de novo designed proteins". Proceedings of the National Academy of Sciences . 112 (40): E5478—E5485. Bibcode : . doi : . PMID .
  17. Mannige, Ranjan (16 May 2017). . PeerJ . 5 . doi : . PMID . Дата обращения: 18 мая 2017 . {{ cite journal }} : Википедия:Обслуживание CS1 (не помеченный открытым DOI) ( ссылка )
  18. . Professor Laurence A. Moran. Дата обращения: 17 января 2013.
  19. . MBU, IISc, Bangalore. Дата обращения: 28 января 2013. Архивировано из 15 января 2013 года.
  20. Lütteke, T. (2005). "Carbohydrate Structure Suite (CSS): analysis of carbohydrate 3D structures derived from the PDB". Nucleic Acids Res . 33 (Database issue): D242—246. doi : . PMID .
  21. Ting, D. (2010). "Neighbor-dependent Ramachandran probability distributions of amino acids developed from a hierarchical Dirichlet process model". PLOS Computational Biology . 6 (4): e1000763. Bibcode : . doi : . PMID . {{ cite journal }} : Википедия:Обслуживание CS1 (не помеченный открытым DOI) ( ссылка )

Дальнейшее чтение

Ссылки


Источник —

elizabeth
  • 2021-07-06
  • 2
  • Tags:

Same as Карта Рамачандрана

The title for the last searches