Interested Article - Перестановка

- 2021-12-08
- 2

В комбинаторике перестано́вкой заданного конечного множества (все элементы различны) называется произвольный упорядоченный набор всех элементов (без повторений). Группируя эти элементы в разном порядке, можно получить различные перестановки. Всего из множества с элементами можно получить ( - факториал ) различных перестановок (см. рисунок) .
Перестановка является частным случаем размещения , когда выбираются все элементы множества .
Подстановка
Перестановку можно рассматривать как функцию, которая каждому элементу некоторой начальной перестановки сопоставляет соответствующий по номеру элемент данной перестановки. Такую функцию часто называют подстановкой . Перестановка множества может быть наглядно представлена в виде таблицы:
где и .
Пример : перестановка элементов множества в обратном порядке:
Инверсией в перестановке называется всякая пара индексов такая, что и . Чётность числа инверсий в перестановке определяет чётность перестановки . Пример:
Здесь элементы 2 и 3 образуют инверсию.
Связанные определения
Носитель перестановки — это подмножество множества , определяемое как
Неподвижной точкой перестановки является всякая неподвижная точка отображения , то есть элемент множества Множество всех неподвижных точек перестановки является дополнением её носителя в .
Специальные типы перестановок
- Тождественная перестановка — перестановка которая каждый элемент отображает в себя:
- Инволюция — перестановка которая является обратной самой себе, то есть
- Беспорядок — перестановка без неподвижных точек .
- Циклом длины называется такая подстановка которая тождественна на всём множестве кроме подмножества и Обозначается .
- Транспозиция — перестановка элементов множества , которая меняет местами два элемента. Транспозиция является циклом длины 2.
Произведения циклов и знак перестановки
Перестановку можно представить в виде ориентированного графа, где вершинами являются элементы конечного множества, а связи между вершинами описывают переход. В случае, , для элемента рисуется петля. Таким образом, получается граф, где из каждой вершины выходит и входит одно ребро. Пример перестановки представленной в виде ориентированного графа можно увидеть на изображении справа.
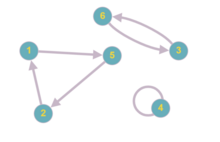
Таким образом, любая перестановка может быть разложена в произведение ( композицию ) непересекающихся циклов длины , причём единственным образом с точностью до порядка следования циклов в произведении. Например:
Часто также считают, что неподвижные точки перестановки представляют собой самостоятельные циклы длины 1, и дополняют ими цикловое разложение перестановки. Для приведённого выше примера таким дополненным разложением будет . Число циклов разной длины, а именно набор чисел , где — это число циклов длины , определяет цикловую структуру перестановки. При этом величина равна длине перестановки, а величина равна общему числу циклов. Число перестановок из элементов с циклами даётся числом Стирлинга первого рода без знака .
Любой цикл может быть разложен в произведение (не обязательно непересекающихся) транспозиций . При этом цикл длины 1 (являющийся по сути тождественной перестановкой ) можно представить как транспозиций или, например, как квадрат любой транспозиции: Цикл длины можно разложить в произведение транспозиций следующим образом:
Разложение циклов на произведение транспозиций не является единственным:
Таким образом, любая перестановка может быть разложена в произведение транспозиций. Хотя это можно сделать многими способами, чётность числа транспозиций во всех таких разложениях одинакова. Это позволяет определить знак перестановки ( чётностью перестановки или сигнатурой перестановки ) как:
где — число транспозиций в каком-то разложении . При этом называют чётной перестановкой , если , и нечётной перестановкой , если .
Эквивалентно, знак перестановки определяется её цикловой структурой: знак перестановки из элементов, состоящий из циклов, равен
- .
Знак перестановки также может быть определён через число инверсий в :
- .
Вариации и обобщения
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка . (Другие авторы подстановкой называют (приведённый выше) наглядный способ записи перестановки. Более существенное отличие состоит в том, что подстановка — это непосредственно функция, а перестановка — результат применения этой функции к элементам последовательности.)
Композиция определяет операцию произведения на перестановках одной длины: Относительно этой операции множество перестановок из элементов образует группу , которую называют симметрической и обычно обозначают .
Любая конечная группа порядка изоморфна некоторой подгруппе симметрической группы ( теорема Кэли ). При этом каждый элемент сопоставляется с перестановкой , задаваемой на элементах тождеством где — групповая операция в .
Перестановки с повторением
Рассмотрим элементов различных типов, причём в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением . Если — число элементов -го типа, то и число всевозможных перестановок с повторениями равно мультиномиальному коэффициенту
Перестановку с повторениями можно также рассматривать как перестановку мультимножества мощности .
Случайная перестановка
Случайной перестановкой называется случайный вектор все элементы которого принимают натуральные значения от 1 до и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой называется такая случайная перестановка , для которой:
для некоторых таких, что:
Если при этом не зависят от , то перестановку называют одинаково распределённой . Если же нет зависимости от , то есть то называют однородной .
См. также
Примечания
- ↑ Выгодский М. Я. Справочник по элементарной математике. — М. : АСТ, 2006. — С. 293—294. — 509 с. — ISBN 5-17-009554-6 .
- Виленкин Н.Я. Глава III. Комбинаторика кортежей и множеств. Размещения с повторениями // . — М. : Наука, 1975. — С. 80. — 208 с. 14 октября 2010 года.
- .
Литература
- Дональд Кнут . Искусство программирования, том 3. Сортировка и поиск = The Art of Computer Programming, vol.3. Sorting and Searching. — 2-е изд. — М. : , 2007. — 824 с. — ISBN 0-201-89685-0 .
- Кострикин А. И. . — М. : Физматлит , 1994. — С. -71. — 320 с. — ISBN 5-02-014644-7 .
- Перестановка // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия , 1984. — Т. 4. — Стб. 256. — 1216 с.
- Сергей Мельников. // Delphi и Turbo Pascal на занимательных примерах. — БХВ-Петербург, 2012. — 448 с. — ISBN 978-5-94157-886-3 .
Ссылки
- // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб. , 1890—1907.
- 2021-12-08
- 2















































































































