Квантовая механика
История Математические основы
Основа Классическая механика Постоянная Планка Интерференция Бра и кет Гамильтониан Старая квантовая теория
Фундаментальные понятия Квантовое состояние Квантовая наблюдаемая Волновая функция Квантовая суперпозиция Квантовая запутанность Смешанное состояние Измерение Неопределённость Принцип Паули Дуализм Декогеренция Симметрия Теорема Эренфеста Туннельный эффект
Эксперименты Опыт Дэвиссона — Джермера Опыт Франка — Герца Опыт Штерна — Герлаха Опыт Юнга Квантовый ластик Квантовый ластик с отложенным выбором Проверка неравенств Белла Фотоэффект Эффект Комптона
Формулировки Представление Шрёдингера Представление Гейзенберга Представление взаимодействия Матричная квантовая механика Интегралы по траекториям Диаграммы Фейнмана
Уравнения Шрёдингера Паули Клейна — Гордона Дирака Швингера — Томонаги фон Неймана Блоха Линдблада Гейзенберга
Интерпретации Копенгагенская Теория скрытых параметров Супердетерминизм Многомировая Теория де Бройля — Бома
Развитие теории Квантовая теория поля Квантовая электродинамика Теория Глэшоу — Вайнберга — Салама Квантовая хромодинамика Стандартная модель Квантовая гравитация
Сложные темы Релятивистская квантовая механика Квантовая теория поля Квантовая гравитация Теория всего
Известные учёные Планк Эйнштейн Шрёдингер Гейзенберг Йордан Бор Паули Дирак Фок Борн де Бройль Ландау Фейнман Бом Эверетт
См. также История возникновения ЭПР-парадокс
См. также: Портал:Физика

В представлении фазового пространства квантовая механика трактует единообразно как координаты , так и импульсы частиц, которые образуют фазовое пространство , в отличие от трактовки Шредингера , где используется координатное или импульсное представления (см. ). Два ключевых элемента физической картины в представлении фазового пространства состоят в следующем: квантовое состояние описывается квазивероятностным распределением (вместо волновой функции , векторами состояний или матрицей плотности ), и оператор умножения заменяется звёздочным произведением .

Теория была полностью разработана Хилбрандом Груневолдом в 1946 году в своей кандидатской диссертации и независимо Джо Моялем . Каждая из этих работ базировались на более ранних идеях, сформулированных Германом Вейлем и Юджином Вигнером .

Главное преимущество квантовой механики в представлении фазового пространства заключается в том, что оно делает квантовую механику аналогичной гамильтоновой механике , избегая формализма операторов, тем самым «освобождая» квантование от «бремени» Гильбертова пространства . Эта формулировка носит статистический характер и предлагает логические связи между квантовой механикой и классической статистической механикой, что позволяет естественное сравнение между ними в так называемом классическом пределе, то есть при ${\displaystyle \hbar \rightarrow 0}$ . Квантовая механика в фазовом пространстве часто выступает в определённых приложениях квантовой оптики (см. ), при изучении декогеренции и целом ряде специальных технических проблем, хотя этот формализм редко используется на практике .

Концептуальные идеи, лежащие в основе развития квантовой механики в фазовом пространстве, воплотились в математических ответвлениях, таких как алгебраическая теория деформирования (см. ) и некоммутативная геометрия .

Распределение в фазовом пространстве

Распределение в фазовое пространстве f ( x , p ) , которое описывает квантовое состояние это . В представлении фазового пространства, распределение можно рассматривать как основополагающее, примитивное описание квантовой системы, без каких-либо ссылок на волновые функции или матрицы плотности .

Существует несколько различных способов представления распределений, но все они взаимосвязаны . Наиболее примечательным является представление Вигнера , W ( x , p ) , обнаруженое первым. Другие представления (приблизительно в порядке убывания распространённости в литературе) включают , , представление Кирквуда — Рихачека, представление Мехты, представление Ривьера и представление Борна — Иордана . Эти альтернативы наиболее полезны, когда гамильтониан принимает особую форму, например при в P представления Глаубера — Сударшана. Поскольку представление Вигнера является самым распространенным в литературе, то в этой статье, как правило, рассматривается оно, если не указано иное.

Распределение в фазовом пространстве обладает свойствами подобными плотности вероятности в 2n-мерном фазовом пространстве. Например, оно является вещественнозначным , в отличие от комплекснозначной волновой функции. Мы можем понимать вероятность, нахождения внутри координатного интервала. Например, путем интегрирования функция Вигнера по всем импульсам и по координатам в интервале [ a , b ] получим:

${\displaystyle \operatorname {P} [a\leq X\leq b]=\int _{a}^{b}\int _{-\infty }^{\infty }W(x,p)\,dp\,dx.}$

Если Â ( x , p ) — оператор, представляющий наблюдаемую величину, то ему можно сопоставить в фазовом пространстве, величину A ( x , p ) через преобразование Вигнера . Наоборот, этот оператор можно восстановить через преобразование Вейля .

Среднее значение наблюдаемой по отношению к распределению в фазовом пространстве задаётся выражением

${\displaystyle \langle {\hat {A}}\rangle =\int A(x,p)W(x,p)\,dp\,dx.}$

Однако, несмотря на внешнее сходство, W ( x , p ) не обладает всеми свойствами подлинного совместного распределения вероятностей , потому что области под ним не являются взаимно исключающими, как требуется в четвёртой аксиоме теории вероятности (аксиома аддитивности). Кроме того, оно может, в общем случае, принимать даже для чистых состояний, за уникальным исключением сжатых когерентных состояний и, соответственно, нарушать вторую аксиому Колмогорова .

Области с такими отрицательными значениями «малы»: они не могут распространяться на компактные области больше, чем несколько ħ, и, следовательно, исчезают в классическом пределе. Они защищены неопределенностью Гейзенберга , которая не позволяет точно локализовать частицу в пределах области фазового пространства меньше, чем ħ, и, таким образом, делает такие «отрицательные вероятности» менее парадоксальными. Если левую часть уравнения можно интерпретировать как среднее значение в гильбертовом пространстве по отношению к оператору, то в контексте квантовой оптики это уравнение известно как . (Подробнее о свойствах и интерпретации функции Вигнера, смотрите главную статью .)

Альтернативный подход к квантовой механике в фазовом пространстве стремится определить волновую функцию (не только квазивероятностной плотности) на фазовом пространстве, обычно с помощью . Для совместимости с принципом неопределенности, волновая функция в фазовом пространстве не может быть произвольной функцией, иначе частицу можно было бы локализовать в сколь угодно малой области фазового пространства. Скорее, преобразование Сегала — Бергмана является голоморфной функцией от x + ip . Существует квазивероятностная плотность, связанная с волновой функцией в фазовом пространстве; это Q представление Хусими волновой функции в координатном представлении.

Звёздочное произведение

Фундаментальный некоммутативный бинарный оператор в фазовом пространстве, который заменяет стандартный оператор умножения — это звёздочное произведение , обозначаемое символом ★ . Каждое представление распределения в фазовом пространстве имеет различные звёздочные произведения. Для конкретности, здесь рассматривается звёздочное произведение, соответствующее представлению Вигнера — Вейля.

Для удобства вводятся обозначения для правой и левой производных . Для пары функций f и g левая и правая производные определяются как

${\displaystyle f{\overleftarrow {\partial }}_{x}g={\frac {\partial f}{\partial x}}\cdot g}$

${\displaystyle f{\overrightarrow {\partial }}_{x}g=f\cdot {\frac {\partial g}{\partial x}}.}$

Дифференциальное определение звёздочного произведения

${\displaystyle f\star g=f\,\exp {\left({\tfrac {i\hbar }{2}}({\overleftarrow {\partial }}_{x}{\overrightarrow {\partial }}_{p}-{\overleftarrow {\partial }}_{p}{\overrightarrow {\partial }}_{x})\right)}\,g,}$

где аргумент экспоненциальной функции представляется в виде степенного ряда. Введённые дифференциальные соотношения позволяют записать это выражение в виде разницы в аргументах f и g :

${\displaystyle {\begin{aligned}(f\star g)(x,p)&=f\left(x+{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{p},p-{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{x}\right)\cdot g(x,p)\\&=f(x,p)\cdot g\left(x-{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{p},p+{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{x}\right)\\&=f\left(x+{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{p},p\right)\cdot g\left(x-{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{p},p\right)\\&=f\left(x,p-{\tfrac {i\hbar }{2}}{\overrightarrow {\partial }}_{x}\right)\cdot g\left(x,p+{\tfrac {i\hbar }{2}}{\overleftarrow {\partial }}_{x}\right).\end{aligned}}}$

Также возможно переписать ★ -произведение как конволюцию, через преобразование Фурье :

${\displaystyle (f\star g)(x,p)={\frac {1}{\pi ^{2}\hbar ^{2}}}\,\int f(x+x',p+p')\,g(x+x'',p+p'')\,\exp {\left({\tfrac {2i}{\hbar }}(x'p''-x''p')\right)}\,dx'dp'dx''dp''~.}$

Таким образом, например, гауссианы преобразуются через гиперболическую функцию

${\displaystyle \exp \left(-{a}(x^{2}+p^{2})\right)~\star ~\exp \left(-{b}(x^{2}+p^{2})\right)={1 \over 1+\hbar ^{2}ab}\exp \left(-{a+b \over 1+\hbar ^{2}ab}(x^{2}+p^{2})\right),}$

или

${\displaystyle \delta (x)~\star ~\delta (p)={2 \over h}\exp \left(2i{xp \over \hbar }\right),}$

и т. д..

Собственные состояния гамильтониана для распределений известны как «звёздочные состояния», ★ - состояния или ★ - собственные функции , а соответствующие им собственные значения известны как звёздочные собственные значения или ★ - собственные значения . Эти решения находятся аналогично как для стационарного уравнения Шрёдингера, используя уравнения для ★ -собственных значений ,

${\displaystyle H\star W=E\cdot W,}$

где H — гамильтониан, простая функция в фазовом пространстве обычно аналогичная классическому гамильтониану.

Эволюция во времени

распределения в фазовом пространстве задаётся квантовой модификацией лиувиллевского потока . Эта формула является результатом применения преобразования Вигнера к версии квантового уравнения Лиувилля для матрицы плотности или уравнением фон Неймана .

В любом представлении распределения в фазовом пространстве со своим ассоциированным звёздочным произведением эволюция во времени определяется уравнением

${\displaystyle {\frac {\partial f}{\partial t}}=-{\frac {1}{i\hbar }}\left(f\star H-H\star f\right),}$

или для функции Вигнера в частности

${\displaystyle {\frac {\partial W}{\partial t}}=-\{\{W,H\}\}=-{\frac {2}{\hbar }}W\sin \left({{\frac {\hbar }{2}}({\overset {\leftarrow }{\partial _{x}}}{\overset {\rightarrow }{\partial _{p}}}-{\overset {\leftarrow }{\partial _{p}}}{\overset {\rightarrow }{\partial _{x}}})}\right)\ H=-\{W,H\}+O(\hbar ^{2}),}$

где {{ , }} — скобки Мояля , преобразование Вигнера квантового коммутатора, а { , } — классические скобки Пуассона .

Это чёткий пример принципа соответствия : это уравнение явно сводится к классическому уравнению Лиувилля в пределе ħ → 0. Однако в квантовом потоке, плотность точек в фазовом пространстве не сохраняется, и вероятностная жидкость становится «диффузионной» и "сжимаемой" . Таким образом, концепция траектории квантовой частицы не определяется точно. Учитывая ограничения, установленные принципом неопределенности в отношении локализации, Нильс Бор отрицал физическое существование таких траекторий в микроскопическом масштабе. С помощью формальных траекторий в фазовом пространстве, временное уравнение для функции Вигнера можно строго решить с помощью метода интегралов по траекториям и , хотя есть неустранимые практические препятствия в обоих случаях. См. фильм для потенциала Морзе, ниже, чтобы оценить быстрое распространение потенциальных траекторий.

Примеры

Простой гармонический осциллятор

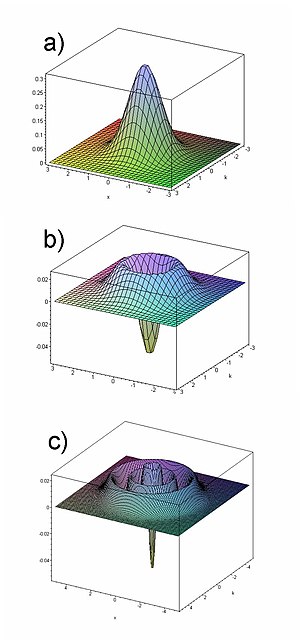
Гамильтониан для простого гармонического осциллятора в одномерном случае в представлении Вигнера — Вейля равен

${\displaystyle H={\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}.}$

Уравнение на ★ -собственные значений для статической функции Вигнера имеет вид

${\displaystyle {\begin{aligned}H\star W&=\left({\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}\right)\star W\\&=\left({\frac {1}{2}}m\omega ^{2}\left(x+{\frac {i\hbar }{2}}{\stackrel {\rightarrow }{\partial }}_{p}\right)^{2}+{\frac {1}{2m}}\left(p-{\frac {i\hbar }{2}}{\stackrel {\rightarrow }{\partial }}_{x}\right)^{2}\right)~W\\&=\left({\frac {1}{2}}m\omega ^{2}\left(x^{2}-{\frac {\hbar ^{2}}{4}}{\stackrel {\rightarrow }{\partial }}_{p}^{2}\right)+{\frac {1}{2m}}\left(p^{2}-{\frac {\hbar ^{2}}{4}}{\stackrel {\rightarrow }{\partial }}_{x}^{2}\right)\right)~W\\&\,\,\,\,\,+{\frac {i\hbar }{2}}\left(m\omega ^{2}x{\stackrel {\rightarrow }{\partial }}_{p}-{\frac {p}{m}}{\stackrel {\rightarrow }{\partial }}_{x}\right)~W\\&=E\cdot W.\end{aligned}}}$

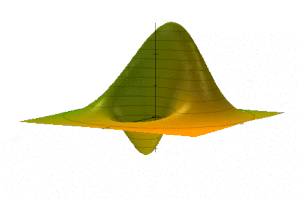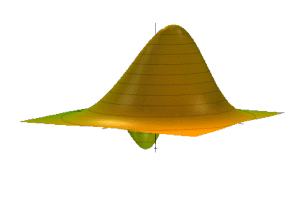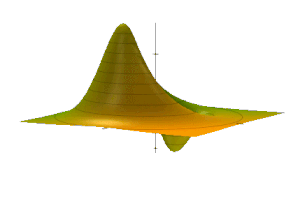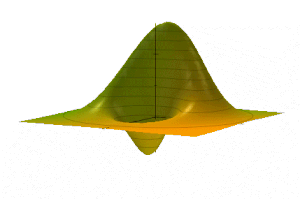
Рассмотрим сначала мнимую часть уравнения на ★ -собственные значения.

${\displaystyle {\frac {\hbar }{2}}\left(m\omega ^{2}x{\overrightarrow {\partial }}_{p}-{\frac {p}{m}}{\overrightarrow {\partial }}_{x}\right)\cdot W=0}$

Это означает, что можно записать ★ -собственные значения как функцию одного аргумента,

${\displaystyle W(x,p)=F\left({\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}\right)\equiv F(u).}$

С этой заменой переменных, можно записать действительную часть уравнения на ★ -собственные значения в форме модифицированного уравнения Лагерра (не Эрмита), решения которого включают в себя полиномы Лагерра в виде

${\displaystyle F_{n}(u)={\frac {(-1)^{n}}{\pi \hbar }}L_{n}\left(4{\frac {u}{\hbar \omega }}\right)e^{-2u/\hbar \omega }~,}$

введенные Груневолдом в его статье , которые соответствуют ★ -собственным значениям

${\displaystyle E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right)~.}$

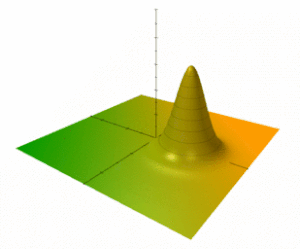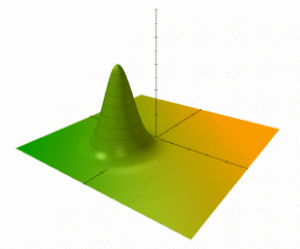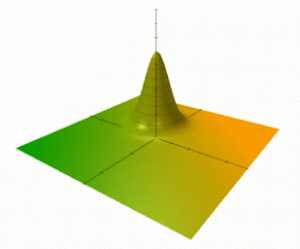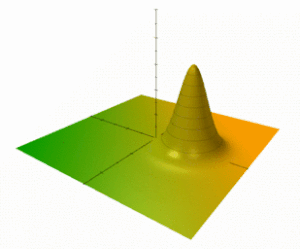
Для гармонического осциллятора эволюция во времени произвольного распределения Вигнера тривиальна. Начальная функция W ( x , p ; t =0) = F ( u ) развивается во времени с помощью приведенного выше уравнения для гамильтониана осциллятора — она просто жёстко вращается в фазовом пространстве,

${\displaystyle W(x,p;t)=W(m\omega x\cos \omega t-p\sin \omega t,~p\cos \omega t+\omega mx\sin \omega t;0)~.}$

Как правило, «холм» (или когерентное состояние) энергии E ≫ ħω может представлять макроскопическую величину и выглядит как классический объект, равномерно вращающийся в фазовом пространстве и напоминает простой механический осциллятор (см. Анимированные фигуры). Интегрируя по всем фазам (начальные позиции при t = 0) таких объектов, непрерывный «палисад», дает не зависящую от времени конфигурацию, аналогичную приведенным выше статическим ★ -состояниям F ( u ) и интуитивную визуализацию для систем с большим действием.

Угловой момент свободной частицы

Предположим, что частица первоначально находится в минимально неопределенном гауссовском состоянии , причем ожидаемые значения положения и импульса центрированы в начале координат в фазовом пространстве. Функция Вигнера для такого свободно распространяющегося состояния,

${\displaystyle W(\mathbf {x} ,\mathbf {p} ;t)={\frac {1}{(\pi \hbar )^{3}}}\exp {\left(-\alpha ^{2}r^{2}-{\frac {p^{2}}{\alpha ^{2}\hbar ^{2}}}\left(1+\left({\frac {t}{\tau }}\right)^{2}\right)+{\frac {2t}{\hbar \tau }}\mathbf {x} \cdot \mathbf {p} \right)}~,}$

где α — параметр, описывающий начальную ширину гауссиана и τ = m / α ² ħ .

Первоначальное положение и импульсы некоррелированы. Таким образом, в трех измерениях мы ожидаем, что векторы положения и импульса будут в два раза более вероятно расположены перпендикулярно друг другу, чем параллельно.

Однако положение и импульс становятся все более коррелированными по мере того, как состояние эволюционирует во времени, поскольку части распределения дальше от центра соответствуют большему импульсу: асимптотически

${\displaystyle W\longrightarrow {\frac {1}{(\pi \hbar )^{3}}}\exp \left[-\alpha ^{2}\left(\mathbf {x} -{\frac {\mathbf {p} t}{m}}\right)^{2}\right]\,.}$

Это относительное « сжатие » отражает распространение пакета свободной волны в координатном пространстве.

Действительно, можно показать, что кинетическая энергия частицы становится асимптотически радиальной только в согласии со стандартным квантовомеханическим представлением о ненулевом угловом моменте основного состояния, определяющем независимость от направления:

${\displaystyle K_{rad}={\frac {\alpha ^{2}\hbar ^{2}}{2m}}\left({\frac {3}{2}}-{\frac {1}{1+(t/\tau )^{2}}}\right)}$

${\displaystyle K_{ang}={\frac {\alpha ^{2}\hbar ^{2}}{2m}}{\frac {1}{1+(t/\tau )^{2}}}~.}$

Потенциал Морзе

Потенциал Морзе используется для аппроксимации колебательной структуры двухатомной молекулы.

Квантовое туннелирование

Туннелирование — это ключевой квантовый эффект, когда квантовая частица, не обладающая достаточной энергией для пролёта выше барьера, все же проходит через него. Этот эффект не существует в классической механике.

Потенциал четвёртой степени

Состояние кота Шрёдингера

Ссылки