Interested Article - Индексы Миллера
- 2021-04-20
- 1
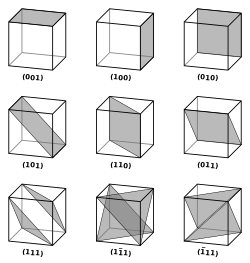
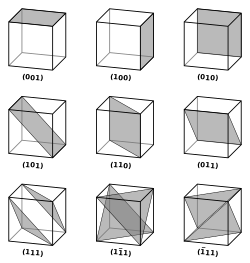
Индексы Миллера — кристаллографические индексы, характеризующие расположение атомных плоскостей в кристалле. Индексы Миллера связаны с отрезками, отсекаемыми выбранной плоскостью на трёх осях кристаллографической системы координат (не обязательно декартовой ). Таким образом, возможны три варианта относительного расположения осей и плоскости:
- плоскость пересекает все три оси
- плоскость пересекает две оси, а третьей параллельна
- плоскость пересекает одну ось и параллельна двум другим
Индексы Миллера выглядят как три взаимно простых целых числа, записанные в круглых скобках: (111), (101), (110)…
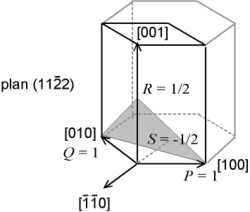
Для работы с гексагональными решётками удобно использовать четырёхсимвольные индексы Миллера — Браве ( hkil ), в которых третий элемент i означает удобную, но вырожденную (не несущую никакой дополнительной информации) компоненту, равную − h − k . Угол между компонентами h , i и k индекса составляет 120°, так что они не ортогональны. Компонента l перпендикулярна всем трём направлениям h , i и k .
Определение индексов Миллера
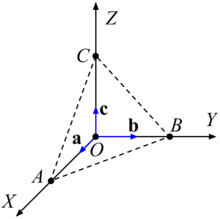
Пусть на осях системы координат ( OXYZ ) решетки кристалла (см. рис. "Система координат решетки кристалла"), плоскость, индексы Миллера которой хотим найти, отсекает отрезки A , на оси X , B , на оси Y , C , на оси Z . Для каждой из осей заданы свои параметры решетки a , b , c . Тогда индексы будут находиться следующим образом. Находим значение отрезков A , B , C в осевых единицах, т. е. необходимо найти A / a , B / b , C / c (полученные величины не имеют размерности). Далее, находим обратные значения найденных величин, т. е. a / A , b / B , c / C . Следующим шагом необходимо найти наименьшее общее кратное чисел: НОК( A / a , B / b , C / c ) или, что то же самое, [ A / a , B / b , C / c ], при этом нужно понимать, что НОК величина положительная, поэтому должно всегда выполняться: НОК( A / a , B / b , C / c ) > 0. Таким образом, индексы Миллера h , k , l будут определяться следующим образом:
;
;
.
Пример .
Имеем, что A / a = 1, B / b = 2, C / c = -4. Найдем НОК( A / a , B / b , C / c ). Заметим, что 1 = 2⁰, 2 = 2¹, 4 = 2², поэтому НОК( A / a , B / b , C / c ) = 4, тогда h = 4, k = 2, l = -1, т. е. ( hkl ) = (42 1 ).
См. также
Ссылки
-
 На
Викискладе
есть медиафайлы по теме
На
Викискладе
есть медиафайлы по теме
- Блинов Ю. Ф., Серба П. В., Московченко Н. Н. . Таганрогский государственный радиотехнический университет. Дата обращения: 11 апреля 2011. 28 марта 2012 года.
- 2021-04-20
- 1
![{\displaystyle h={\frac {a}{A}}\cdot \left[{\frac {A}{a}},\,{\frac {B}{b}},\,{\frac {C}{c}}\right]}](/images/005/147/5147486/4.jpg?rand=342797)
![{\displaystyle k={\frac {b}{B}}\cdot \left[{\frac {A}{a}},\,{\frac {B}{b}},\,{\frac {C}{c}}\right]}](/images/005/147/5147486/5.jpg?rand=369848)
![{\displaystyle l={\frac {c}{C}}\cdot \left[{\frac {A}{a}},\,{\frac {B}{b}},\,{\frac {C}{c}}\right]}](/images/005/147/5147486/6.jpg?rand=763569)