Interested Article - Теория катастроф
- 2021-02-01
- 1
Теория катастроф — раздел математики , включающий в себя теорию бифуркаций дифференциальных уравнений ( динамических систем ) и теорию особенностей гладких отображений. Теория катастроф — раздел современной математики, который является дальнейшим развитием теории устойчивости и бифуркаций.
Термины «катастрофа» и «теория катастроф» были введены Рене Томом и Кристофером Зиманом в конце 1960-х — начале 1970-х годов («катастрофа» в данном контексте означает резкое качественное изменение объекта при плавном количественном изменении параметров, от которых он зависит) .
Теория катастроф нашла многочисленные применения в различных областях прикладной математики, физики, а также в экономике и политологии .
В технических вузах изучается теория устойчивости, которая является основой теории катастроф. Методы теории устойчивости находят применение в теории автоматического управления, моделировании динамических систем, в электротехнике, биологии, когнитивных науках.
История
Первые фундаментальные результаты в области динамических систем, относящиеся к теории катастроф, принадлежат Анри Пуанкаре (метод нормальных форм в теории дифференциальных уравнений) и Александру Андронову-старшему (бифуркации динамических систем). Основы теории особенностей гладких отображений были заложены прежде всего в трудах американского тополога Хасслера Уитни в 1940-х — 1950-х годы, которым предшествовала лемма Морса о нормальной форме функции в окрестности невырожденной критической точки.
В конце 1960-х годов развитием этого направления занялся Рене Том . Однако популярность идеи Уитни и Тома приобрели благодаря нескольким публикациям Зимана в 1970-х годов, который активно пропагандировал теорию катастроф, сравнивая её значение с изобретением математического анализа и говоря о «революции в математике». Бурное развитие теории катастроф в 1970-е — 1990-е годы связано с деятельностью Майкла Бордмана , ( нем. ), ( англ. ), Джона Мазера , ( фр. ), Рене Тома, Терри Уолла , Кристофера Зимана и особенно Владимира Арнольда и его учеников ( , Александра Варченко , Виктора Васильева , Александра Гивенталя , Виктора Горюнова , Сабира Гусейн-Заде , Владимира Закалюкина , Максима Казаряна , ).
Семь элементарных катастроф по Тому
Теория катастроф анализирует критические точки (репетиции) потенциальной функции, то есть точки, где не только первая производная функции равна нулю, но и равны нулю же производные более высокого порядка. Динамика развития таких точек может быть изучена при помощи разложения потенциальной функции в рядах Тейлора посредством малых изменений входных параметров. Если точки роста складываются не просто в случайный узор, но формируют структурированную область стабильности, эти точки существуют как организующие центры для особых геометрических структур с низким уровнем катастрофичности, с высоким уровнем катастрофичности в окружающих их областях фазового пространства. Если потенциальная функция зависит от трёх или меньшего числа активных переменных, и пяти или менее активных параметров, то в этом случае существует всего семь обобщённых структур описанных геометрий бифуркаций, которым можно приписать стандартные формы разложений в ряды Тейлора, в которые можно разложить репетиции при помощи диффеоморфизма (гладкой трансформации, обращение которой также гладко). Сегодня эти семь фундаментальных типов катастроф известны под именами, которые им дал Рене Том.
Потенциальные функции с одной активной переменной
Катастрофа типа «складка»

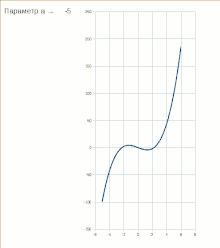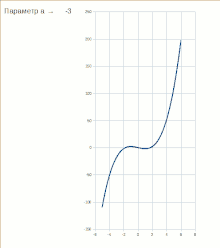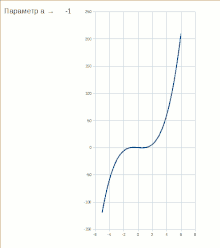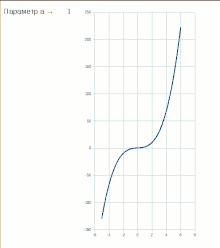
Стабильная и нестабильная части экстремума, исчезаемого при бифуркации типа «складка»:
- .
При отрицательных значениях параметра потенциальная функция имеет два экстремума — один стабильный (устойчивое равновесие) и один нестабильный (неустойчивое равновесие). Если параметр медленно изменяется, система может находиться в точке стабильного минимума. Но если , стабильные и нестабильный экстремумы встречаются и аннигилируют. Это — точка бифуркации. При не существует стабильного решения.
Если физическая система проходит через точку бифуркации типа «складка», и поэтому параметр проходит через нулевое значение, стабильность решения при теряется, и система может осуществить внезапный переход в новое, весьма отличное от предыдущего состояние. Это бифуркационное значение параметра иногда называется «точкой фиксации».
| Пример кода на Python |
import time
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
from matplotlib import style
style.use('ggplot')
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
values = [-6.0, -5.0, -4.0, -3.0, -2.0, -1.0, 0.0, 1.0]
points = [[-6, -3], [-5, -2.5], [-4, -2], [-3, -1.5], [-2, -1.0], [-1, -0.5],
[0, 0], [1, 0.5], [2, 1.0], [3, 1.5], [4, 2.0], [5, 2.5], [6, 3]]
def calc_fold_data(x, a):
x3 = np.power(x, 3)
result = x3 + (a * x)
return result
def animate(index):
if index == len(values):
time.sleep(3)
exit()
value = values[index]
xar = []
yar = []
for point in points:
x = calc_fold_data(point[0], value)
y = calc_fold_data(point[1], value)
print("Y: {} X:{}".format(x, y))
xar.append(x)
yar.append(y)
ax1.clear()
plt.title("Value: {}".format(value))
plt.scatter(0, 0)
ax1.plot(xar, yar)
ani = animation.FuncAnimation(fig, animate, interval=1000)
plt.show()
|
Катастрофа типа «сборка»

|
|

|

|
Диаграмма катастрофы «сборка» с точкой возврата, на которой показаны кривые (коричневые, красные) по переменной x , удовлетворяющие выражению для параметров ( a , b ), кривые показаны для непрерывно изменяющегося параметра b при различных значениях параметра a . Вне геометрического места точек возврата (синяя область) для каждой точки ( a , b ) в фазовом пространстве существует только одно экстремальное значение переменной x . Внутри точек возврата существует два различных значения x , которые дают локальные минимумы функции V ( x ) для каждой пары ( a , b ). При этом указанные значения разделены локальным максимумом.
Бифуркация типа «вилка» при a = 0 на пространстве b = 0. Форма точек возврата в фазовом пространстве ( a , b ) около точки катастрофы, показывающая геометрическое место бифуркаций типа «свёртка», которое разделяет область с двумя стабильными решениями и область с одним решением. Геометрия точек возврата весьма обычна, когда производится изучение того, что происходит с бифуркациями типа «свёртка» при добавлении в управляющее пространство нового параметра b. Изменяя параметры, можно найти, что имеется кривая (синяя) точек в пространстве ( a , b ), на которой теряется стабильность, то есть на этой кривой стабильное решение может внезапно «перепрыгнуть» на альтернативное значение (также стабильное).
Но в геометрии точек возврата кривая бифуркаций заворачивает назад, создавая вторую ветвь, на которой уже это второе решение теряет стабильность, а потому может совершить «прыжок» назад на исходное множество решений. При повторном увеличении значения параметра b и последующем уменьшении его, можно наблюдать гистерезис в поведении петель, поскольку система следует по одному решению, «перепрыгивает» на другое, следует по нему и «перепрыгивает» назад на исходное.
Однако это возможно только в области в параметрическом пространстве при a < 0. Если значение параметра a увеличивается, петли гистерезиса становятся меньше и меньше, пока значение a не достигнет 0. В этой точке петли исчезают (катастрофа с точкой возврата), и появляется только одно стабильное решение.
Также можно рассмотреть процесс изменения параметра a при неизменном значении b . В симметричном случае при b = 0 можно наблюдать бифуркацию типа «вилы» при уменьшающемся значении параметра a одно стабильное решение внезапно разделяется на два стабильных решения и одно нестабильное. В это время физическая система проходит в область a < 0 через точку возврата ( a = 0, b = 0) (это пример спонтанного нарушения симметрии). Вдали от точки возврата не существует внезапных изменений в физической системе, поскольку при прохождении по кривой бифуркации свёртки происходит только то, что становится доступным второе альтернативное решение.
Одно из наиболее интересных предложений по использованию катастрофы с точкой возврата заключается в том, что этот тип катастрофы можно использовать для моделирования поведения собаки, которая в ответ на внешнее воздействие может испугаться или обозлиться. Предложение заключается в том, что при умеренном воздействии ( a > 0) собака будет проявлять плавное изменение отклика с испуга на злость в зависимости от того, как было проведено воздействие. Но более высокий уровень воздействия — это стресс, соответствующий переходу в область a < 0. В этом случае если собака изначально испугалась, она останется испуганной при увеличении уровня воздействия на неё, пока в конечном итоге она не достигнет точки возврата, где произойдёт спонтанный переход в режим злобы. При переходе в этот режим собака будет оставаться озлобленной даже в случае постепенного снижения воздействия на неё.
Другой пример прикладного применения катастрофы с точкой возврата заключается в моделировании поведения электрона при перемещении с одного энергетического уровня на другой, что часто наблюдается в химических и биологических системах. Это указывает на то, что бифуркации рассмотренного типа и геометрия точек возврата является наиболее важной практической частью теории катастроф. Это шаблоны, которые проявляются вновь и вновь в физике, инженерии и математическом моделировании.
Оставшиеся простые геометрии катастроф являются более специализированными по сравнению с только что рассмотренной, а потому проявляются только в некоторых отдельных случаях.
Катастрофа типа «ласточкин хвост»

Управляющее пространство в данном типе катастроф является трёхмерным. Каскад бифуркаций в фазовом пространстве состоит из трёх поверхностей бифуркаций типа «складка», которые встречаются на двух кривых бифуркаций с точками возврата, которые в конечном итоге встречаются в одной точке, представляющей собой бифуркацию типа «ласточкин хвост».
По мере прохождения значений параметров по поверхностям областей бифуркаций типа «складка» пропадает один минимум и один максимум потенциальной функции. В области бифуркаций с точкой возврата два минимума и один максимум замещаются одним минимумом; за ними бифуркации типа «складка» исчезают. В точке ласточкиного хвоста два минимума и два максимума встречаются в одном значении переменной x . Для значений a > 0 за ласточкиным хвостом существует либо одна пара (минимум, максимум), либо не существует вообще никаких бифуркаций. Это зависит от значений параметров b и c . Две поверхности бифуркаций типа «складка» и две линии бифуркаций с точками возврата встречаются при a < 0, а потому исчезают в самой точке ласточкиного хвоста, заменяясь одной поверхностью бифуркаций типа «складка». Последняя картина Сальвадора Дали под названием «Ласточкин хвост» создана под влиянием этого типа катастроф.
Катастрофа типа «бабочка»
В зависимости от значений параметров потенциальная функция может иметь три, два или один локальный минимум, причём все минимумы разделены областями с бифуркациями типа «складка». В точке с поэтичным наименованием «бабочка» встречаются три различные пространства (трёхмерных плоскости) таких бифуркаций типа «складка», две поверхности бифуркаций с точками возврата и кривая бифуркаций типа «ласточкин хвост». Все эти бифуркации пропадают в одной точке и преобразуются в простую структуру с точкой возврата тогда, когда значение параметра a становится положительным.
Потенциальные функции с двумя активными переменными
Омбилические катастрофы являются примерами катастроф второго порядка. Они, к примеру, могут наблюдаться в оптике при отражении света от трёхмерных поверхностей. Сами по себе такие катастрофы тесно связаны с геометрией почти сферических поверхностей. Рене Том предложил рассматривать гиперболическую омбилическую катастрофу как разрушение волны, а эллиптическую омбилическую катастрофу ― как процесс создания структур, похожих на волосяной покров.
Гиперболическая омбилика
Эллиптическая омбилика
Параболическая омбилика
Запись и классификация катастроф по Арнольду
В. И. Арнольд предложил классификацию катастроф « ADE-классификация », использующую глубокие связи с теорией групп Ли .
- A 0 — несингулярная точка: .
- A 1 — локальный экстремум : устойчивый минимум или неустойчивый максимум .
- A 2 — складка
- A 3 — сборка
- A 4 — ласточкин хвост
- A 5 — бабочка
- A k — бесконечная последовательность форм от одной переменной
- D 4 + — кошелёк = гиперболическая омбилика
- D 4 - — пирамида = эллиптическая омбилика
- D 5 — параболическая омбилика
- D k — бесконечная последовательность других омбилик
- E 6 — символическая омбилика
- E 7
- E 8
В теории сингулярности есть объекты, которые соответствуют большинству других простых групп Ли.
Применения теории катастроф
Создание и развитие этой части математического анализа было связано с широкими возможностями наглядного анализа некоторых сложных явлений, особенно тех, которые встречаются при описании самых разных естественных явлений, в которых также рассматриваются разрывные функции, для которых аппарат математического анализа не подходит ( радуга , каустика , потеря устойчивости конструкций, колебания и разрушение в строительной механике, поведение в этологии , астрофизика, бифуркационная неустойчивость атомной решетки, спонтанный порядок в биохимических реакциях, динамика популяций, гидродинамическая неустойчивость и возникновение турбулентности, хаотическая динамика странного аттрактора).
См. также
Примечания
- Термин катастрофа был введён Томом для обозначения качественного изменения объекта при плавном изменении параметров, от которых он зависит. Этот термин, заменивший использовавшиеся до него термины бифуркация , перестройка , метаморфоза , завоевал широкую популярность после того, как Зиман [121] предложил употреблять название теории катастроф для объединения теории особенностей, теория бифуркаций и их приложений. .
- По инициативе Р. Тома вместо бифуркаций говорят о «катастрофах». Это слова тоже не надо понимать буквально. Приведу примеры, действительно серьёзно рассматривавшиеся в работах по «теории катастроф»: если нарушается устойчивость упругой конструкции, то это, скорее всего, катастрофа, но если солнечные лучи, преломляясь в воде, образуют на дне ручья яркие линии — это едва ли кого-нибудь волнует, кроме разве детей, видящих это впервые. <…> Если катастрофа — синоним бифуркации, то можно спросить, какой термин удачнее. Как ясно из сказанного, ни тот, ни другой не приходится понимать буквально. Но «катастрофа» — слово обычного (литературного и разговорного) языка, имеющее определённый и притом весьма эмоционально окрашенный смысл, а о первоначальном значении слова «бифуркация» знает намного меньше людей, и даже у них с ним едва ли связаны какие-то эмоции. Поэтому для науки более подходит нейтральное слово «бифуркация», а для массовых изданий — «катастрофа». [Д. В. Аносов. О развитии теории динамических систем за последнюю четверть века]. Одной из главных задач теории катастроф является получение так называемой нормальной формы исследуемого объекта (дифференциального уравнения или отображения) в окрестности «точки катастрофы» и построенная на этой основе классификация объектов
Литература
На русском языке
- Арнольд В. И. / Рец.: А. В. Чернавский . — 3-е изд., доп. — М. : Наука . Гл. ред. физ.-мат. лит., 1990. — 128 с. — 84 000 экз. — ISBN 5-02-014271-9 .
- В. И. Арнольд .
- В. И. Арнольд .
- В. И. Арнольд, В. С. Афраймович, Ю. С. Ильяшенко, Л. П. Шильников .
- В. И. Арнольд, В. А. Васильев, В. В. Горюнов, О. В. Ляшко .
- В. И. Арнольд, В. А. Васильев, В. В. Горюнов, О. В. Ляшко .
- А. Б. Гивенталь .
- В. М. Закалюкин .
- Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений, — Любое издание.
- Арнольд В. И. Особенности каустик и волновых фронтов, — М.: Фазис, 1996.
- Брёкер Т., Ландер Л. Дифференцируемые ростки и катастрофы, — Любое издание.
- Голубицкий М., Гийемин В. Устойчивые отображения и их особенности, — М.: Мир, 1977.
- Постон Т., Стюарт И. Теория катастроф и её приложения, — М.: Мир, 1980.
- Том Р. Структурная устойчивость и морфогенез, — М.: Логос, 2002.
- Брус Дж., Джиблин П. Кривые и особенности: Геометрическое введение в теорию особенностей, — М.: Мир, 1988.
- Павлова Н.Г., Ремизов А.О. . — М. : Изд-во МФТИ, 2022. — 181 с. — ISBN 978-5-7417-0794-4 .
На английском языке
- Arnold, Vladimir Igorevich. Catastrophe Theory, 3rd ed. Berlin: Springer-Verlag, 1992.
- Gilmore, Robert. Catastrophe Theory for Scientists and Engineers. New York: Dover, 1993.
- Postle, Denis. Catastrophe Theory — Predict and avoid personal disasters. Fontana Paperbacks 1980. ISBN 0-00-635559-5
- Poston, Tim and Stewart, Ian. Catastrophe Theory and Its Applications. London, San Francisco, Melbourne: Pitman, 1978
- Poston, T. and Stewart, Ian. Catastrophe: Theory and Its Applications. New York: Dover, 1998. ISBN 0-486-69271-X .
- Sanns, Werner. Catastrophe Theory with Mathematica: A Geometric Approach. Germany: DAV, 2000.
- Saunders, Peter Timothy. An Introduction to Catastrophe Theory. Cambridge, England: Cambridge University Press, 1980.
- Thom, René. Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Reading, MA: Addison-Wesley, 1989. ISBN 0-201-09419-3 .
- Thompson, J. Michael T. Instabilities and Catastrophes in Science and Engineering. New York: Wiley, 1982.
- Woodcock, Alexander Edward Richard and Davis, Monte. Catastrophe Theory. New York: E. P. Dutton, 1978.
- Zeeman, E.C. Catastrophe Theory-Selected Papers 1972—1977. Reading, MA: Addison-Wesley, 1977.
Ссылки
На русском языке
- Д. В. Аносов.
На английском языке
- 2021-02-01
- 1