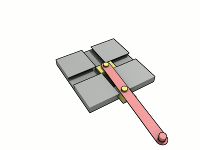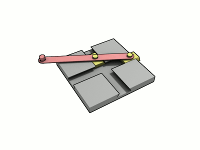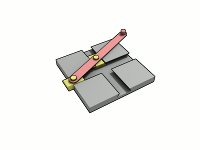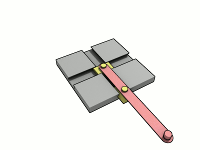
Эллипсограф или Сеть Архимеда — это механизм, который способен преобразовывать возвратно-поступательное движение в эллипсоидное .

Общая информация

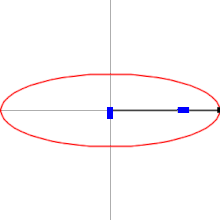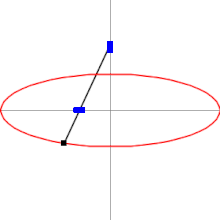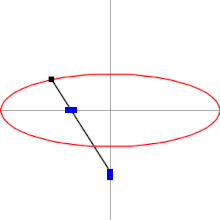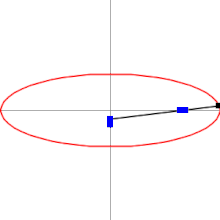
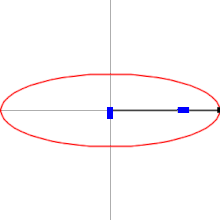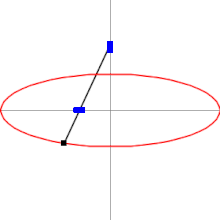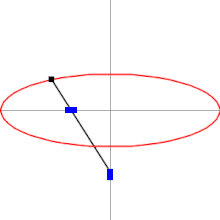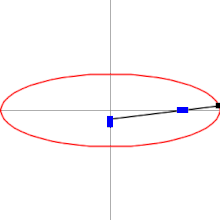
Эллипсограф состоит из двух ползунов, которые могут двигаться по двум перпендикулярным канавкам или направляющим. Ползуны прикреплены к стержню посредством шарниров , и находятся на фиксированном расстоянии друг от друга вдоль стержня. Ползуны движутся вперёд и назад — каждый по своей канавке, — и конец стержня описывает эллипс на плоскости. Полуоси эллипса a и b представляют собой расстояния от конца стержня до шарниров на ползунах. Обычно расстояния a и b можно варьировать, и тем самым менять форму и размеры описываемого эллипса.

В более общем случае направляющие, по которым движутся ползуны, могут быть не перпендикулярны друг другу, и точки A , B и C могут образовывать треугольник. Результирующая траектория точки C останется эллипсом .

Этот механизм применяется в качестве чертёжного инструмента, а также для разрезания стекла, картона, фанеры и других листовых материалов.

История этого механизма точно не определена, но считается, что эллипсографы существовали ещё во времена Диадоха или даже во времена Архимеда .

Математическое описание

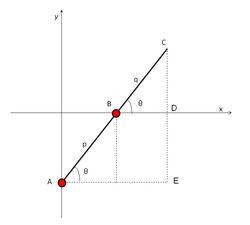
Пусть C — это конец стержня, и A , B — шарниры на ползунах. Пусть p и q — расстояния от A до B , и от B до C , соответственно. Координатные оси y и x проведём таким образом, что движение ползунов A и B будет происходить вдоль этих осей, соответственно. Когда стержень образует угол θ с осью x , координаты точки C определяются уравнениями

${\displaystyle x=(p+q)\cos \theta }$

${\displaystyle y=q\sin \theta }$

Эти уравнения представляют собой параметрические уравнения эллипса. Нетрудно вывести и уравнение получающегося эллипса в декартовой системе координат .

См. также

• Шарнирные методы построения лемнискаты Бернулли
• Шотландский механизм

Примечания

Литература

• J. W. Downs: Practical Conic Sections: The Geometric Properties of Ellipses, Parabolas and Hyperbolas . Courier Dover 2003, ISBN 978-0-486-42876-5 , p. 4-5

Ссылки

• игрушек, сделанных из кирпичиков «Лего»