Проекти́вная пло́скость — двумерное проективное пространство . Важным частным случаем является вещественная проективная плоскость .

Проективная плоскость отличается важной ролью, которую играет так называемая аксиома Дезарга , в проективных пространствах больших размерностей являющаяся теоремой.

Определения

Проективная плоскость над телом

Проективная плоскость над телом ${\displaystyle K}$ — это множество одномерных подпространств (прямых, проходящих через ноль) трёхмерного линейного пространства ${\displaystyle K^{3}}$ . Данные прямые называются точками проективной плоскости. Проективная плоскость над телом ${\displaystyle K}$ обычно обозначается ${\displaystyle K\mathrm {P} ^{2}}$ , например ${\displaystyle \mathbb {R} \mathrm {P} ^{2}}$ , ${\displaystyle \mathbb {C} \mathrm {P} ^{2}}$ , ${\displaystyle \mathbb {H} \mathrm {P} ^{2}}$ и так далее.

Аксиоматическое определение

Классическая проективная плоскость П определяется следующими аксиомами. Первые четыре из них являются обязательными.

• П1. Через две различные точки P и Q плоскости П проходит прямая, причём только одна.
• П2. Любые две прямые имеют общую точку.
• П3. Существуют три точки, не лежащие на одной прямой.
• П4. Каждая прямая содержит не менее трёх точек.

Дополнительными аксиомами являются следующие:

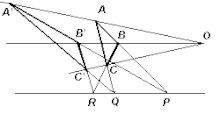
• П5. Аксиома Дезарга. Если треугольники ABC и A’B’C' таковы, что прямые AA' , BB' и CC' пересекаются в точке O , то точки пересечения пар соответствующих сторон AB и A’B' (P) , BC и B’C' (R) , AC и A’C'(Q) лежат на одной прямой.
• П6. Аксиома Паппа. Если l и l' — две различные прямые, A,B,С — три различные точки на прямой l , а A',B',C' — три различные точки l', причём все эти точки отличны от О — точки пересечения прямых l и l' , то точки пересечения пар соответствующих сторон AB' и A’B (P) , BC' и B’C (R) , AC' и A’C (Q) лежат на одной прямой.
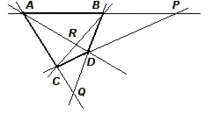
• П7. Аксиома Фано. Пусть A, B, C, D — точки, никакие три из которых не лежат на одной прямой. Проведём все шесть прямых, соединяющих эти точки (AB, AC, AD, BC, BD, CD) . Обозначим точку пересечения AB и CD через P, AC и BD через Q и AD и BC через R (диагональные точки). Эти диагональные точки не лежат на одной прямой.

Примеры

• Вещественная проективная плоскость .
• Плоскость Фано
• Плоскость Молтона — пример недезарговой проективной плоскости.

Свойства

• Для любой проективной плоскости над телом выполняются аксиомы П1—П4 и аксиома Дезарга П5. Обратно, если в плоскости П выполняется аксиома Дезарга П5, то она есть проективная плоскость над некоторым телом ${\displaystyle K}$ .

• Если выполняются аксиома Паппа П6 и аксиомы П1—П4, то выполняется и аксиома Дезарга П5. В этом случае П является проективной плоскостью над полем (то есть тело K коммутативно). Обратно, в любой проективной плоскости над полем выполняется аксиома Паппа.

• Если выполняются аксиомы П1—П4 и аксиома Дезарга П5, то аксиома Фано П7 выполняется тогда и только тогда, когда П является проективной плоскостью над телом ${\displaystyle K}$ характеристики ≠2.

Топология вещественной проективной плоскости

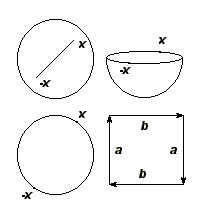
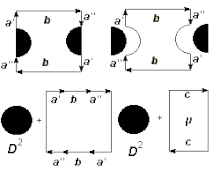
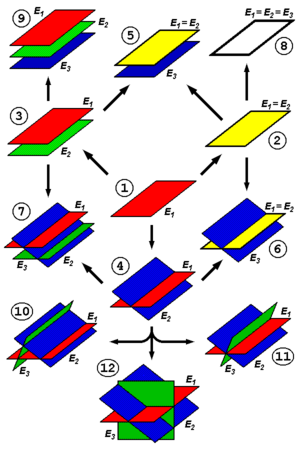
Представим вещественную проективную плоскость P²( R ) как множество прямых в R³ . Её точки образуют пучок всех прямых, проходящих через начало координат. Построим единичную сферу. Тогда каждая наша прямая (точка P²( R )) пересекает сферу в двух противоположных точках: x и -x . Из этого легко получается другая модель. Отбросим верхнюю полусферу z > 0 . Каждой точке на отброшенной полусфере соответствует точка на нижней полусфере, а диаметрально противоположные точки на экваториальной окружности нижней полусферы отождествляются. «Выпрямляя» полусферу, получаем круг, у которого отождествлены диаметрально противоположные точки граничной окружности. Круг гомеоморфен квадрату, противоположные стороны которого отождествляются (в направлении стрелок). Как показано на следующем рисунке, этот квадрат гомеоморфен кругу D² с приклеенным листом Мёбиуса μ. Поэтому проективная плоскость неориентируема .

Цикл (полуокружность) от ${\displaystyle -x}$ до ${\displaystyle x}$ (обозначим его как ${\displaystyle a}$ ) не является границей, однако полная окружность от ${\displaystyle -x}$ до ${\displaystyle x}$ и от ${\displaystyle x}$ до ${\displaystyle -x}$ (обозначим его как ${\displaystyle 2a}$ ) уже ограничивает всю «внутреннюю» часть проективной плоскости, поэтому 2 ${\displaystyle a}$ ≈0, а ${\displaystyle a}$ ≠0 (знак равенства означает, гомологичен или нет цикл нулю), то есть любой негомологичный нулю цикл гомологичен циклу ${\displaystyle a}$ . Поэтому одномерная группа гомологий состоит из двух элементов H ₁ (P²)={0,1} , где нулевому элементу группы соответствуют одномерные циклы, гомологичные нулю, а единице — все циклы гомологичные ${\displaystyle a}$ .

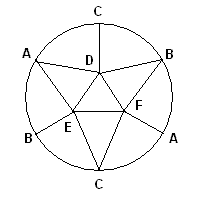
Группы гомологий проективной плоскости легко вычисляются: ${\displaystyle H_{0}=\mathbb {Z} }$ , ${\displaystyle H_{1}=\mathbb {Z} /2}$ и ${\displaystyle H_{2}=0}$ . Числа Бетти (ранги групп гомологий) равны соответственно b ₀ =1, b ₁ =0, b ₂ =0 . Эйлерова характеристика равна знакочередующейся сумме χ(P²)=b ₀ -b ₁ +b ₂ =1 . Можно вычислить эйлерову характеристику и непосредственно из триангуляции χ(P²) (см. нижний рисунок) — число вершин равно 6, ребер 15 и граней 10, значит χ(P²)=6-15+10=1 .

Согласно известной теореме о классификации поверхностей среди всех компактных , связных , замкнутых гладких многообразий проективная плоскость однозначно определяется тем, что она неориентируема и её эйлерова характеристика равна 1 .

Фундаментальная группа π ₁ (P²)= Z ₂ , высшие гомотопические группы соответствуют таковым для сферы π _n (P²)=π _n (S²) для n≥2 .

См. также

• Лента Мёбиуса
• Бутылка Клейна
• Поверхность Боя — пример погружения вещественной проективной плоскости в трёхмерное евклидово пространство.

Литература

• Артин Э. Геометрическая алгебра. — М.: Наука, 1969
• Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы и приложения. — М.: Наука, 1979
• Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы теории гомологий. — М.: Наука, 1984
• Кокстер Г. С. М. Действительная проективная плоскость. -М:Физматгиз, 1959
• Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966
• Фоменко А. Т. Наглядная геометрия и топология. — М.: МГУ, 1998
• Хартсхорн Р. Основы проективной геометрии. — М.: Мир, 1970