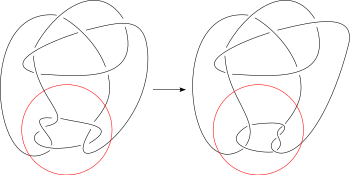
В теории узлов мутация — это специальный вид . Мутация выбирает маленькую часть узла и либо отражает, либо поворачивает её, вследствие чего получается некий новый (возможно исходный) узел, который называется мутантом исходного.

Определение

Пусть K — узел, заданный в виде ^* . Пусть D — диск в плоскости диаграммы, границы которого пересекают K ровно четыре раза. Можно считать (в случае необходимости используем изотопию), что диск геометрически круглый и четыре точки пересечения расположены на равном расстоянии. Часть узла внутри диска называется диаграммой . Имеется два отражения, которые меняют местами пары концов нитей на диаграмме этого тэнгла. Кроме того, имеются также вращения. Мутация заменяет исходный тэнгл на тэнгл, полученный любой из этих операций. В результате получается узел, который называется мутацией узла K .

Пару узлов, связанных мутацией, называют узлами-мутантами или просто мутантами . Здесь слово «мутант» используется в значении «результат мутации» и всегда имеет отношение сразу к двум узлам. Пример использования: Узел ${\displaystyle K}$ мутант узла ${\displaystyle Q}$ , узлы ${\displaystyle K}$ и ${\displaystyle Q}$ мутанты (по отношению друг к другу).

Свойства

• Если один мутант тривиален , то и другой тривиален. Иными словами, из тривиального узла мутацией можно получить только тривиальный узел, или, что равносильно, тривиальный узел является изолированной вершиной в мутации.

• Многие классические инварианты у мутантов совпадают, поэтому нередко задача различения двух узлов, связанных мутацией, оказывается достаточно сложной. Так, например, узлы-мутанты имеют одинаковый гиперболический объём (результат Рубемана), Многочлен Александера , , гомологии , и многочлен HOMFLY .

• Однако группа узла и род могут различить мутантов.

Примеры

• Пара узлов, Конвея и Киношиты-Терасака, являются мутантами друг друга, но имеют различный род , равный 3 и 2 соответственно.

Примечания

Литература

• Adams C. C. (англ.) . — New York: American Mathematical Society , 2004. — 307 p. — ISBN 978-0821836781 .

• Cromwell P. R. (англ.) . — Cambridge: Cambridge University Press , 2004. — 328 p. — ISBN 9780511809767 .

• Livingston C. (англ.) . — The Mathematical Association of America , 1996. — Vol. 24. — 258 p. — (The Carus Mathematical Monographs). — ISBN 978-0883850275 .

• Morton H. R. (англ.) // New ideas in low dimensional topology. — 2015. — P. 379-412 . — doi : .

Для улучшения этой статьи желательно : Проверить качество перевода с иностранного языка. После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.