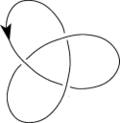
В теории узлов обратимый узел — это узел , который может быть непрерывной деформацией переведён в себя, но с обратной ориентацией. Необратимый узел — это любой узел, который не имеет такого свойства. Обратимость узла является инвариантом узла . Обратимое зацепление — это зацепление с таким же свойством.

Существует только пять типов симметрии узлов, определяемые хиральностью и обратимостью — полностью хиральный, двухсторонний, положительно ахиральный необратимый, отрицательно ахиральный необратимый и полностью ахиральный обратимый .

История вопроса

Давно известно, что большинство простых узлов , таких как трилистник и восьмёрка , обратимы. В 1962 году ( англ. ) высказал предположение, что некоторые узлы необратимы, но не было доказано их существование, пока в 1963 году Хейл Троттер не обнаружил бесконечное семейство необратимых кружевных зацеплений . Теперь известно, что почти все узлы необратимы .

Обратимые узлы

Все узлы с числом пересечений 7 и менее обратимы. Не известно общего метода, который дал бы ответ обратим узел или нет . Проблему можно перевести в алгебраическую терминологию , но, к сожалению, не известно алгоритма решения этой алгебраической задачи.

Если узел обратим и ахирален , он полностью ахирален. Простейший узел с этим свойством — это восьмёрка. Хиральные обратимые узлы классифицируются как двухсторонние .

Строго обратимые узлы

Более абстрактный способ определения обратимого узла — сказать, что существует гомеоморфизм 3-сферы , переводящий узел в себя, но меняющий ориентацию узла на противоположную. Если использовать вместо гомеоморфизма более строгое условие — инволюцию — получим определение строго обратимого узла. Все узлы с единица, такие как трилистник и восьмёрка , строго обратимы .

Необратимые узлы

Простейшим примером необратимого узла служит 8 ₁₇ (в обозначениях Александера — Бриггса) или .2.2 (в обозначениях Конвея). Кружевной узел 7, 5, 3 необратим, как и все кружевные узлы вида (2 p + 1), (2 q + 1), (2 r + 1), где p , q и r — различные целые, что даёт бесконечное семейство узлов, необратимость которых доказана Троттером .

См. также

• Хиральный узел

Примечания

Литература

• Jim Hoste, Morwen Thistlethwaite, Jeff Weeks. The first 1,701,936 knots // The Mathematical Intelligencer. — 1998. — Т. 20 , вып. 4 . — doi : . 15 декабря 2013 года.
• H.F. Trotter. Topology. — Pergamon Press, 1963. — Т. 2. — doi : .
• Kunio Murasugi. Knot Theory and Its Applications. — Springer, 2007. — ISBN 9780817647186 .
• Greg Kuperberg. Detecting knot invertibility // Journal of Knot Theory and its Ramifications. — 1996. — Т. 5 , вып. 2 . — doi : . — arXiv : .
• W. Edwin Clark, Mohamed Elhamdadi, Masahico Saito, Timothy Yeatman. Quandle colorings of knots and applications. — 2013. — arXiv : .
• Kanji Morimoto. There are knots whose tunnel numbers go down under connected sum // Proceedings of the American Mathematical Society. — 1995. — Т. 123 , вып. 11 . — doi : . — JSTOR .

Внешние ссылки

• Jablan, Slavik & Sazdanovic, Radmila. , LinKnot .
• , Nrich.Maths.org .