В теории узлов кружевное зацепление (или крендельное зацепление ) — это специальный вид зацепления . Кружевное зацепление, являющееся также узлом (то есть зацеплением с одной компонентой), называется кружевным узлом , крендельным узлом или просто кренделем .

В стандартной проекции кружевное зацепление ${\displaystyle (p_{1},\,p_{2},\dots ,\,p_{n})}$ имеет ${\displaystyle p_{1}}$ левосторонних скруток в первом , ${\displaystyle p_{2}}$ во втором и, в общем случае, ${\displaystyle p_{n}}$ в n -ом.

Кружевное зацепление можно описать как с целым числом переплетений.

Некоторые базовые результаты

Кружевное зацепление ${\displaystyle (p_{1},p_{2},\dots ,p_{n})}$ является узлом тогда и только тогда, когда и ${\displaystyle n}$ , и все ${\displaystyle p_{i}}$ являются или в точности одно из чисел ${\displaystyle p_{i}}$ чётно .

Кружевное зацепление ${\displaystyle (p_{1},\,p_{2},\dots ,\,p_{n})}$ является , если по меньшей мере два ${\displaystyle p_{i}}$ равны нулю. Однако обратное неверно.

Кружевное зацепление ${\displaystyle (-p_{1},-p_{2},\dots ,-p_{n})}$ является отражением кружевного зацепления ${\displaystyle (p_{1},\,p_{2},\dots ,\,p_{n})}$ .

Кружевное зацепление ${\displaystyle (p_{1},\,p_{2},\dots ,\,p_{n})}$ эквивалентно (то есть гомотопически эквивалентно на S ³ ) кружевному зацеплению ${\displaystyle (p_{2},\,p_{3},\dots ,\,p_{n},\,p_{1})}$ . Тогда, также, кружевное зацепление ${\displaystyle (p_{1},\,p_{2},\dots ,\,p_{n})}$ эквивалентно кружевному зацеплению ${\displaystyle (p_{k},\,p_{k+1},\dots ,\,p_{n},\,p_{1},\,p_{2},\dots ,\,p_{k-1})}$ .

Кружевное зацепление ${\displaystyle (p_{1},\,p_{2},\,\dots ,\,p_{n})}$ эквивалентно кружевному зацеплению ${\displaystyle (p_{n},\,p_{n-1},\dots ,\,p_{2},\,p_{1})}$ . Однако если ориентировать зацепление в каноническом виде, эти два зацепления имеют противоположную ориентацию.

Примеры

Кружевной узел (1, 1, 1) — это (правосторонний) трилистник , а узел (−1, −1, −1) является его зеркальным отражением.

Кружевной узел (5, −1, −1) — это стивидорный узел (6 ₁ ).

Если p , q и r являются различными нечётными числами, большими 1, то кружевной узел ( p , q , r ) является необратимым .

Кружевное зацепление (2 p , 2 q , 2 r ) — это зацепление, образованное тремя связанными тривиальными узлами .

Кружевной узел (−3, 0, −3) ( прямой узел ) является связной суммой двух трилистников .

Кружевное зацепление (0, q , 0)) — это тривиального узла с другим узлом.

Зацепление Монтесиноса

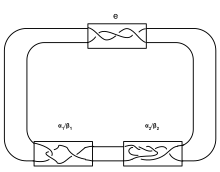
Зацепление Монтесиноса — это специальный вид зацепления , обобщающее кружевные зацепления (кружевное зацепление можно считать зацеплением Монтесиноса с целыми переплетениями). Зацепление Монтесиноса, являющееся также узлом (то есть, зацепление с однлй компонентой) является узлом Монтесиноса .

Зацепление Монтесиноса состоит из нескольких . Одним из обозначений зацепления Монтесиноса является ${\displaystyle K(e;\alpha _{1}/\beta _{1},\alpha _{2}/\beta _{2},\ldots ,\alpha _{n}/\beta _{n})}$ .

В этих обозначениях ${\displaystyle e}$ и все ${\displaystyle \alpha _{i}}$ и ${\displaystyle \beta _{i}}$ являются целыми числами. Зацепление Монтесиноса, заданное таким обозначением, состоит из рациональных плетений, заданных целым числом ${\displaystyle e}$ , и рациональных плетений ${\displaystyle \alpha _{1}/\beta _{1},\alpha _{2}/\beta _{2},\ldots ,\alpha _{n}/\beta _{n}}$

Использование

Кружевные зацепления (−2, 3, 2 n + 1) особенно полезны при изучении 3-многообразий . В частности, для этих многообразий многие результаты были установлены на основе на .

Гиперболический объём дополнения кружевного зацепления (−2,3,8) равен учетверённой постоянной Каталана , примерно 3,66. Это кружевное зацепление является одним из двух гиперболических многообразий с двумя каспами с минимальными возможными объёмами, второе многообразие является дополнением зацепления Уайтхеда .

Примечания

Литература

• Ian Agol . The minimal volume orientable hyperbolic 2-cusped 3-manifolds // Proceedings of the American Mathematical Society . — 2010. — Т. 138 , вып. 10 . — doi : .

Литература для дальнейшего чтения

• Hale F. Trotter . // Topology. — Pergamon Press, 1963. — Т. 2. — С. 275—280.
• Akio Kawauchi. A survey of knot theory. — Birkhäuser, 1996. — ISBN 3-7643-5124-1 .
• Heiner Zieschang. Classification of Montesinos knots // Topology / A. Dold, B. Eckmann/Ludwig D.Faddeev, Arkadii A. Mal’cev. General and Algebraic Topology, and Applications. Proceeding of the International Topological Conference held in Leningrad, August 23-27, 1982. — Berlin Heidelberg: Springer, 1984. — Т. 1060. — (Lecture Notes in Mathematics/USSR). — ISBN 3-540-13337-2 . — ISBN 0-387-13337-2 .