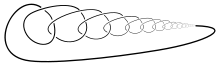
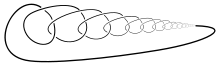
Дикий узел — патологическое вложение окружности в пространство.

Дикие узлы можно найти в некоторых кельтских узорах. ^{[ источник не указан 2900 дней ]}

Определение

Узел называется ручным , если он может быть «утолщён», то есть если существует его расширение до полнотория S ¹ × D ² , допускающего вложение в 3-сферу . В теории узлов и в теории 3-многообразии часто слово «ручной» опускается.

Узлы, не являющиеся ручными, называются ди́кими и могут иметь патологическое поведение.

Примеры

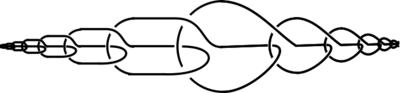
Дикими являются узлы, содержащие так называемые — некоторые простые дуги, полученные диким вложением в ${\displaystyle E^{3}}$ . Например, для дуги ${\displaystyle L_{1}}$ фундаментальная группа ${\displaystyle p_{1}}$ ( ${\displaystyle E^{3}L}$ ) нетривиальна, для дуги ${\displaystyle L_{2}}$ группа ${\displaystyle {\pi }_{1}(E^{3}/L)}$ тривиальна, но само ${\displaystyle E^{3}/L}$ не гомеоморфно дополнению в ${\displaystyle E^{3}}$ к точке .

На рисунке выше приведён дикий узел с одной дикой (патологической) точкой. Легко построить дикий узел, содержащий несколько патологических точек, бесконечное число таких точек, и даже несчётное множество патологических точек. В книге Сосинского приведено построение дикого узла, патологические точки которого образуют канторово множество . Возможно представить и дикий узел, содержащее более сложное множество — ожерелье Антуана .

Свойcтва

• Узел является ручным тогда и только тогда, когда он может быть представлен в виде конечной ломаной .
• Гладкие узлы являются ручными.

Вариации и обобщения

• Нетривиальные дикие узлы появляются и в сферах старших размерностей. Например по теореме о двойной надстройке , двойная надстройка над сферой Пуанкаре гомеоморфна стандартной сфере ${\displaystyle \mathbb {S} ^{5}}$ . При этом экватор двойной надстройки образует в ${\displaystyle \mathbb {S} ^{5}}$ дикой узел и его дополнение имеет нетривиальную фундаментальную группу .

См. также

• Дикая сфера

Примечания

Литература

• L. H. Kauffman. // Transactions of the American Mathematical Society. — American Mathematical Society, 1990. — Vol. 318, № 2 .
• А. Б. Сосинский. Узлы. Хронология одной математической теории. — Москва: МЦНМО, 2005. — ISBN 5-94057-220-0 .