Кусочно-гладкая функция
- 1 year ago
- 0
- 0

Гауссова функция ( гауссиан , гауссиана , функция Гаусса ) — вещественная функция , описываемая следующей формулой:
где параметры — произвольные вещественные числа . Введена Гауссом в 1809 году как функция плотности нормального распределения , и наибольшее значение имеет в этом качестве, в этом случае параметры выражаются через среднеквадратическое отклонение и математическое ожидание :
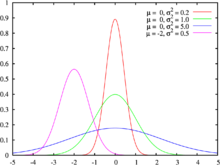
График гауссовой функции при и — колоколообразная кривая, параметр определяет максимальную высоту графика — пик колокола, отвечает за сдвиг пика от нуля (при — пик в нуле), а влияет на ширину (размах) колокола.
Существуют многомерные обобщения функции . Кроме применений в теории вероятностей , статистике и других многочисленных приложениях как функции плотности нормального распределения, гауссиана имеет самостоятельное значение в математическом анализе , математической физике , теории обработки сигналов.
Свойства гауссовой функции связаны с её конструкцией из экспоненциальной функции и вогнутой квадратичной функции , логарифм гауссианы — вогнутая квадратичная функция.
Параметр связан с полушириной колокола графика следующим образом:
Гауссова функция может быть выражена через полуширину колокола графика следующим образом:
Перегибы — две точки, в которых .
Гауссова функция аналитична , в пределе к обеим бесконечностям стремится к нулю:
Будучи составленной из экспоненциальной функции и арифметических операций, гауссиана является элементарной , однако её первообразная неэлементарна; интеграл гауссовой функции:
— это (с точностью до постоянного множителя) — функция ошибок , являющаяся спецфункцией . При этом интеграл по всей числовой прямой (в связи со свойствами экспоненциальной функции) — константа :
Этот интеграл обращается в единицу только при условии:
и это даёт в точности тот случай, когда гауссиана является функцией плотности нормального распределения случайной переменной с математическим ожиданием и дисперсией .
Произведение гауссиан — гауссова функция; свёртка двух гауссовых функций даёт гауссову функцию, притом параметр свёртки выражается из соответствующих параметров входящих в неё гауссиан: . Произведение двух функций плотности нормального распределения, являясь гауссовой функцией, в общем случае не дает функцию плотности нормального распределения.

Пример двумерного варианта гауссовой функции:
здесь задаёт высоту колокола, определяют сдвиг пика колокола от нулевой абсциссы , а отвечают за размах колокола. Объём под такой поверхностью:
В наиболее общей форме, двумерная гауссиана определяется следующим образом:
где матрица:
Вариант гауссовой функции в -мерном евклидовом пространстве :
где — вектор-столбец из компонентов, — положительно определённая матрица размера , и — операция транспонирования над .
Интеграл такой гауссовой функции над всем пространством :
Возможно определить -мерный вариант и со сдвигом:
где — вектор сдвига, а матрица — симметричная ( ) и положительно определённая.
Супергауссова функция — обобщение гауссовой функции, в которой аргумент экспоненты возводится в степень :
получившая применение для описания свойств гауссовых пучков . В двумерном случае супергауссова функция может быть рассмотрена с различными степенями по аргументам и :
Основное применение гауссовых функций и многомерных обобщений — в роли функции плотности вероятности нормального распределения и многомерного нормального распределения . Самостоятельное значение функция имеет для ряда уравнений математической физики , в частности, гауссианы являются функциями Грина для уравнения гомогенной и изотропной диффузии (соответственно, и для уравнения теплопроводности ), и преобразование Вейерштрасса — операция свёртки обобщённой функции , выражающей начальные условия уравнения, с гауссовой функцией. Также гауссиана является волновой функцией основного состояния квантового гармонического осциллятора .
В вычислительной химии для определения молекулярных орбиталей используются так называемые — линейные комбинации гауссовых функций.
Гауссовы функции и их дискретные аналоги (такие, как ) используются в цифровой обработке сигналов , обработке изображений , синтезе звука ; в частности, через гауссианы определяются и . В определении отдельных видов искусственных нейронных сетей также участвуют гауссовы функции.