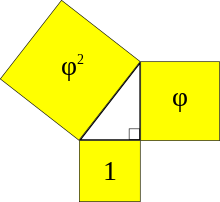
Треугольник Кеплера — это прямоугольный треугольник , длины сторон которого составляют геометрическую прогрессию . При этом соотношение длин сторон треугольника Кеплера связано с золотым сечением

${\displaystyle \varphi ={1+{\sqrt {5}} \over 2}}$

которое может быть записано в виде : ${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$ , или приблизительно 1 : 1.272 : 1.618 Квадраты сторон этого треугольника (см. рисунок) составляют геометрическую прогрессию, соответствующую золотому сечению.

Треугольники с таким соотношением сторон были названы в честь немецкого математика и астронома Иоганна Кеплера (1571—1630), который первым продемонстрировал, что в таких треугольниках отношение длины короткого катета к гипотенузе равно золотому сечению . Таким образом, треугольник Кеплера объединяет в себе два ключевых математических понятия — теорему Пифагора и золотое сечение , по поводу чего Кеплер отметил:

В геометрии существует два сокровища: одно из них — теорема Пифагора, другое — разделение линии в золотой пропорции. Первое мы можем сравнить с массой золота, второе мы можем назвать драгоценным камнем. Иоганн Кеплер

—

Некоторые источники утверждают, что соотношение сторон знаменитых пирамид в Гизе приближается к треугольнику Кеплера .

Следствие

Тот факт, что треугольник со сторонами ${\displaystyle 1}$ , ${\displaystyle {\sqrt {\varphi }}}$ и ${\displaystyle \varphi }$ образует прямоугольный треугольник, прямо следует из переписывания квадратного трёхчлена для золотого сечения ${\displaystyle \varphi }$ :

${\displaystyle \varphi ^{2}=\varphi +1}$

в виде теоремы Пифагора :

${\displaystyle (\varphi )^{2}=({\sqrt {\varphi }})^{2}+(1)^{2}.}$

Отношение к среднему арифметическому, среднему геометрическому и среднему гармоническому

Для положительных вещественных чисел а и b их среднее арифметическое , среднее геометрическое и среднее гармоническое являются длинами сторон прямоугольного треугольника тогда и только тогда, когда треугольник является треугольником Кеплера .

Построение треугольника Кеплера

Треугольник Кеплера может быть построен с помощью циркуля и линейки через построение золотого сечения следующим образом:

1. Построить простой квадрат
2. Провести линию от середины одной стороны квадрата к противоположному углу
3. Использовать эту линию в качестве радиуса дуги, определяющей высоту прямоугольника
4. Дополнить до золотого сечения
5. Использовать длинную сторону прямоугольника золотого сечения в качестве радиуса дуги, которая, пересекая противоположную сторону прямоугольника, задаёт длину гипотенузы треугольника Кеплера.

Сам Кеплер строил этот треугольник по-другому. В письме к своему бывшему учителю, профессору Михаэлю Мёстлину, он писал: «Если на линии, которая разделена в крайнем и среднем отношении, построить прямоугольный треугольник таким образом, что прямой угол будет находиться в точке раздела, то меньшая сторона будет равняться большему сегменту разделенной линии.» .

Математическое совпадение

Возьмём треугольник Кеплера со сторонами ${\displaystyle a,a{\sqrt {\varphi }},a\varphi ,}$ и рассмотрим:

• окружность, которая окружает его, и
• квадрат со стороной, равной средней по величине стороне треугольника.

Тогда периметр квадрата ( ${\displaystyle 4a{\sqrt {\varphi }}}$ ) и длина окружности ( ${\displaystyle a\pi \varphi }$ ) совпадают с точностью до 0,1 %.

Это математическое совпадение ${\displaystyle \pi \approx 4/{\sqrt {\varphi }}}$ . Эти квадрат и окружность не могут иметь одинаковую длину периметра, поскольку в этом случае можно было бы решить классическую неразрешимую задачу о квадратуре круга . Другими словами, ${\displaystyle \pi \neq 4/{\sqrt {\varphi }}}$ поскольку ${\displaystyle \pi }$ — трансцендентное число .

Примечания