Бильярдный компьютер ( англ. Billiard-ball computer ) — логическая модель для проведения обратимых вычислений , механический компьютер , основанный на законах движения Ньютона и предложенный в 1982 году Эдвардом Фредкиным и .

Вместо использования электронных сигналов, как в обычном компьютере архитектуры фон Неймана , он применяет принципы движения бильярдных шаров при отсутствии трения . Бильярдный компьютер может быть использован для изучения связей между обратимыми вычислениями и обратимыми процессами в физике.

Описание

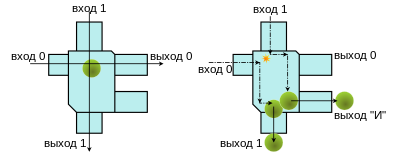
Бильярдный компьютер моделирует булевы логические схемы , используя вместо проводов пути, по которым движутся шары, ограниченные стенками: сигнал кодируется наличием или отсутствием шаров на путях, а логические вентили моделируются при помощи столкновений шаров на пересечениях путей. В частности, можно так подобрать пути шаров, чтобы получить вентиль Тоффоли , универсальный обратимый логический вентиль , с помощью которого можно получить любой другой обратимый логический вентиль. Это означает, что правильно подобранный бильярдный компьютер способен провести любые вычисления .

Моделирование

Бильярдный компьютер можно моделировать, используя различные типы обратимых клеточных автоматов , включая блочные и . В таких моделях шары движутся с постоянной скоростью вдоль осей координат, чего достаточно для моделирования логических схем. Как шары, так и стенки соответствуют некоторым группам живых (содержащих 1) ячеек, а объемлющее поле заполнено мёртвыми (содержащими 0) ячейками .

Также бильярдный компьютер может быть реализован с использованием живых крабов-солдат вида в качестве бильярдных шаров .

Примечания