Блочный лук
- 1 year ago
- 0
- 0
Блочный клеточный автомат — класс клеточных автоматов , в которых решётка разбита на блоки, а функция перехода применяется к каждому блоку по отдельности. Блочные клеточные автоматы полезны для моделирования физических явлений, поскольку часто несложно выбрать функции перехода так, чтобы получившийся клеточный автомат был обратим и подчинялся выбранным законам сохранения .
Клеточный автомат — это регулярная решётка из ячеек, состояние каждой из которых берётся из конечного множества состояний, и функция перехода, необходимая для обновления состояний ячеек, исходя из состояний её соседей. Он называется блочным , если решётка разбита на равные непересекающиеся блоки и функция перехода использует в качестве окрестности каждой ячейки её блок. При этом автомат должен иметь некоторое конечное число разбиений на блоки, используемых поочерёдно: например, одно разбиение может сдвигаться в некотором направлении.
Таким образом, во время каждого шага автомата ко всем ячейкам одновременно применяется функция перехода, которая меняет каждый блок независимо от остальных, потом разбиение меняется на следующее и шаг повторяется. Это позволяет производить нетривиальные вычисления, используя достаточно простые функции перехода.
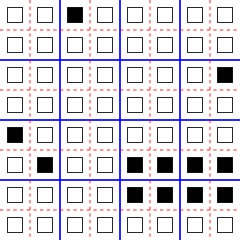
Простейшим примером такой схемы является окрестность Марголуса , в которой ячейки квадратной решётки поделены на блоки 2 × 2 вертикальными и горизонтальными прямыми, а после каждого шага разделение на блоки сдвигается на одну ячейку по горизонтали и вертикали; таким образом, все четыре ячейки любого блока оказываются в разных блоках на следующем шаге. Эта окрестность названа в честь ( англ. Norman Margolus ), одного из первых исследователей блочных клеточных автоматов.
Примером блочного клеточного автомата, использующим окрестность Марголуса, являются «Криттеры» . Функция перехода «Криттеров» меняет состояние каждой ячейки на противоположное, если число живых ячеек в блоке не равняется двум, и вращает на 180° блок целиком, если это число равняется трём. Поскольку число живых ячеек меняется на число мёртвых, а функции перехода при каждом значении числа ячеек обратимы, такой клеточный автомат обратим на каждом блоке, а потому обратим в целом. Тем не менее, он проявляет сложное динамическое поведение, схожее с игрой «Жизнь» Конвея ; в частности, он полон по Тьюрингу , см. подробности в соответствующей статье .