Interested Article - Щёлк

Плитка шоколада 7 × 4 — один из вариантов поля для игры в Щёлк

«Щёлк» ^:407 (от англ. Chomp ) — , заключающаяся в поедании двумя игроками плитки шоколада по определённым правилам.

Современная геометрическая формулировка игры была придумана Дэвидом Гейлом в 1974 году, а более ранняя арифметическая — в 1952 году. Англоязычное название Chomp — буквально означающее «Чавк» (от «чавкать») — придумал Мартин Гарднер .

Геометрическая версия

Поле игры «Щёлк» — прямоугольная плитка шоколада; двое игроков по очереди выбирают одну дольку и съедают вместе со всеми дольками выше и правее её . Проигрывает тот игрок, который съедает «отравленную» левую нижнюю дольку ^:407 .

Ниже приведён пример игры на поле 5 × 3: «отравленная» долька отмечена красным, а съедаемые игроком дольки — пунктиром.

Начало игры		Первый игрок		Второй игрок		Первый игрок		Второй игрок

В этом примере первый игрок вынужден съесть «отравленную» дольку и потому проигрывает.

Арифметическая версия

Поле для случая $N=p^{n}q^{m}$ (другая версия — верх и низ отражены).

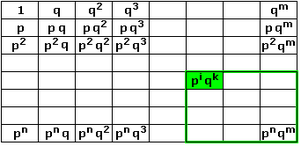
Игру «Щёлк» можно переформулировать арифметически: изначально загадано натуральное число $n$ ; двое игроков по очереди называют делители $n_{1},n_{2},\ldots$ числа $n$ , которые не являются кратными уже названных $n_{i}$ . Проигрывает игрок, вынужденный назвать число 1 .

Для чисел $N$ с факторизацией $p^{k}q^{l}$ , то есть имеющих только два простых делителя , арифметическая версия сводится к геометрической в прямоугольнике (k+1) × (l+1). При этом делителям соответствуют дольки, запрещённым делителям — съеденные дольки, числу 1 — «отравленная» долька, см. таблицу ниже.

9	18	36	72	144
3	6	12	24	48
1	2	4	8	16

Анализ игры

С точки зрения теории игр , «Щёлк» — беспристрастная детерминированная игра с полной информацией . Кроме того, в игре конечное число состояний, а потому из общих утверждений теории игр следует, что у одного из игроков должна быть выигрышная стратегия.

Заимствование стратегии позволяет показать, что выигрышная стратегия есть у первого игрока (кроме случая поля 1 × 1), однако доказательство неконструктивно . В частности, допустим, что у второго игрока существует выигрышная стратегия и докажем, что у первого игрока она также есть, предположив, что первым ходом первый игрок съел только правую верхнюю дольку и рассмотрел ход второго игрока, ведущий к выигрышной стратегии ; тогда первый игрок может сам сделать такой первый ход, тем самым «позаимствовав» стратегию второго игрока. Значит, у второго игрока не может быть выигрышной стратегии, а потому она есть у первого ^:410 .

По состоянию на 1974 год, известны выигрышные стратегии первого только для частных форм поля ^:408 :

Поле квадратно. Первым ходом первый игрок должен откусить квадрат со стороной на один меньше; останутся две полоски шириной 1, соединённые по одной дольке в форме перевёрнутой буквы «Г». Далее первый игрок должен симметрично повторять ходы второго ^:408 .
Поле имеет форму 2 × n. Первым ходом первый игрок должен откусить правую верхнюю дольку. Далее, после каждого хода второго игрока он должен восстанавливать ситуацию, чтобы в нижней строке было на одну дольку больше ^:410 .

Также на компьютере найдены выигрышные стратегии для небольших размеров поля. Наименьший известный размер поля, для которого выигрышная стратегия не единственна — (8, 10) .

Примечания

↑ Гарднер М. Математические новеллы . Пер. с англ. Ю. А. Данилова. Под ред. Я. А. Смородинского. M., «Мир», 1974. 456 с. с илл.; стр. 407—412
В другой версии — ниже и правее.
В другой версии, соответственно, — левую верхнюю.
Winning ways for your mathematical plays , Volume 3 (2nd edn), by E. R. Berlekamp, J. H. Conway and R. K. Guy. Pp. 275. 2018. ISBN 9780429945618 . CRC Press, 2018. Стр. 39
Дольку, противоположную «отравленной»; в другой версии — правую нижнюю.
За исключением случая, когда поле имеет вид 1 × 1 и второй игрок не ходит, потому что первый уже проиграл.
Elwyn R. Berlekamp et al.: Gewinnen — Strategien für mathematische Spiele , Band 3. Vieweg, Braunschweig/Wiesbaden 1986, ISBN 3-528-08533-9 , S. 172f