Медицинская сортировка
- 1 year ago
- 0
- 0
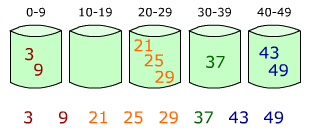
Блочная сортировка (Карманная сортировка, корзинная сортировка, англ. Bucket sort ) — алгоритм сортировки , в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо другим. Затем элементы помещаются обратно в массив . Этот тип сортировки может обладать линейным временем исполнения.
Данный алгоритм требует знаний о природе сортируемых данных, выходящих за рамки функций "сравнить" и "поменять местами", достаточных для сортировки слиянием, сортировки пирамидой, быстрой сортировки, сортировки Шелла, сортировки вставкой.
Преимущества: относится к классу быстрых алгоритмов с линейным временем исполнения O(N) (на удачных входных данных).
Недостатки: сильно деградирует при большом количестве мало отличных элементов, или же на неудачной функции получения номера корзины по содержимому элемента. В некоторых таких случаях для строк, возникающих в реализациях основанного на сортировке строк алгоритма сжатия BWT , оказывается, что быстрая сортировка строк в версии Седжвика значительно превосходит блочную сортировку скоростью.
Если входные элементы подчиняются равномерному закону распределения , то математическое ожидание времени работы алгоритма карманной сортировки является линейным. Это возможно благодаря определенным предположениям о входных данных. При карманной сортировке предполагается, что входные данные равномерно распределены на отрезке [0, 1) .
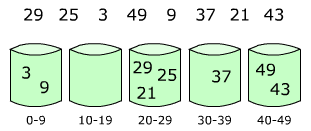
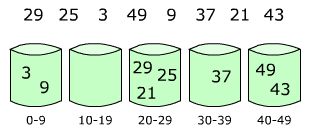
Идея алгоритма заключается в том, чтобы разбить отрезок [0, 1) на n одинаковых отрезков (карманов), и разделить по этим карманам n входных величин. Поскольку входные числа равномерно распределены, предполагается, что в каждый карман попадет небольшое количество чисел. Затем последовательно сортируются числа в карманах. Отсортированный массив получается путём последовательного перечисления элементов каждого кармана.
functiprn bucket-sort(A, n) is
buckets ← новый массив из n пустых элементов
for i = 0 to (length(A)-1) do
вставить A[i] в конец массива buckets[msbits(A[i], k)]
for i = 0 to n - 1 do
next-sort(buckets[i])
return Конкатенация массивов buckets[0], ..., buckets[n-1]
На вход функции bucket-sort подаются сортируемый массив (список, коллекция и т.п.) A и количество блоков - n .
Массив buckets представляет собой массив массивов (массив списков, массив коллекций и т.п.), подходящих по природе к элементам A .
Функция msbits(x,k) тесно связана с количеством блоков - n (возвращает значение от 0 до n), и, в общем случае, возвращает k наиболее значимых битов из x ( floor(x/2^(size(x)-k)) ). В качестве msbits(x,k) могут быть использованы разнообразные функции, подходящие по природе сортируемым данным и позволяющие разбить массив A на n блоков. Например, для символов A-Z это может быть сопоставление номерам букв 0-25, или возврат кода первой буквы (0-255) для ASCII набора символов; для чисел [0, 1) это может быть функция floor(n*A[i]) , а для произвольного набора чисел в интервале [a, b) - функция floor(n*(A[i]-a)/(b-a)) .
Функция next-sort также реализует алгоритм сортировки для каждого созданного на первом этапе блока. Рекурсивное использование bucket-sort в качестве next-sort превращает данный алгоритм в поразрядную сортировку . В случае n = 2 соответствует быстрой сортировке (хотя и с потенциально плохим выбором опорного элемента).
Оценим сложность алгоритма блочной сортировки для случая, при котором в качестве алгоритма сортировки блоков ( next-sort из псевдокода) используется сортировка вставками .
Для оценки сложности алгоритма введём
случайную величину
n
i
, обозначающую количество элементов, которые попадут в карман
B[i]
. Время работы сортировки вставками равно
.
Время работы алгоритма карманной сортировки равно
Вычислим математическое ожидание обеих частей равенства:
Найдем величину .
Введем случайную величину
, которая равна
1
, если
A[j]
попадает в
i
-й карман, и
0
в противном случае:
Если k ≠ j , величины X ij и X ik независимы, поэтому:
Таким образом
Итак, ожидаемое время работы алгоритма карманной сортировки равно