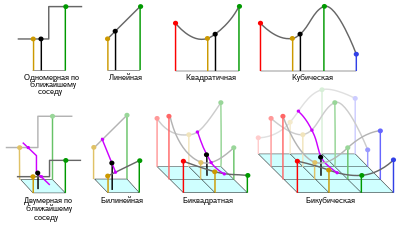
Интерполяция методом ближайшего соседа ( ступенчатая интерполяция ) — метод интерполяции , при котором в качестве промежуточного значения выбирается ближайшее известное значение функции. Интерполяция методом ближайшего соседа является самым простым методом интерполяции.

Связь с диаграммами Вороного

Для заданного множества точек в пространстве диаграммой Вороного называется разбиение пространства на такие области, что для всех точек области ближайшей к ним точкой из заданного множества является одна и та же точка. Это соответствует интерполяции методом ближайшего соседа, так как во всей области будет выбрано одно и то же значение интерполируемой функции.

См. также

• Задача поиска ближайшего соседа
• Округление
• Дискретизация
• Экстраполятор нулевого порядка

Это заготовка статьи о компьютерной графике . Помогите Википедии, дополнив её.

В статье не хватает ссылок на источники (см. рекомендации по поиску ). Информация должна быть проверяема , иначе она может быть удалена. Вы можете статью, добавив ссылки на авторитетные источники в виде сносок . ( 7 июня 2019 )