Релятивистская электродинамика
- 1 year ago
- 0
- 0
Релятивистская квантовая химия — раздел квантовой химии , использующий понятия из области квантовой механики и теории относительности для объяснения и предсказания свойств и структур соединений или атомов . Речь идёт об атомах , электроны которых имеют характерные скорости движения близкие к скорости света (0,2 с и выше). Примером могут служить атомы тяжёлых и сверхтяжёлых элементов .
Первоначально квантовая механика была разработана без учёта теории относительности . «Релятивистскими эффектами» являются расхождения между значениями, рассчитанными с помощью моделей с учётом и без учёта теории относительности. Релятивистские эффекты имеют важное значение для элементов с большими атомными номерами. Например, для лантаноидов и актиноидов .
Начиная с 1935 года, провела релятивистское описание многоэлектронных систем , вопреки сделанному в 1929 году Полем Дираком заявлению, что единственные недостатки, остающиеся в квантовой механике «… приводят к возникновению трудностей только тогда, когда задействованы высокоскоростные частицы, и поэтому не имеют значения при рассмотрении строения атомов и молекул и обычных химических реакций, в которых обычные квантово-механические расчёты, как правило, достаточно точны, если пренебречь релятивистским изменением массы и скорости, и принимать в расчёт только кулоновское взаимодействие между электронами и атомными ядрами» .
Химики-теоретики в целом соглашались с заявлением Дирака вплоть до 1970-х годов, когда появились работы, которые показали реализацию релятивистских эффектов в соединениях тяжёлых элементов . Уравнение Шрёдингера в оригинальной статье 1926 года не учитывала теорию относительности. Релятивистские поправки к уравнению были сделаны позже (см. уравнения Клейна-Гордона-Фока ), чтобы объяснить тонкую структуру атомных спектров. Однако эти и другие поправки к уравнению Шрёдингера не сразу получили распространение в химическом сообществе. Поскольку атомные спектры разрабатывались в значительной степени в области физики, а не химии, большинство химиков не были знакомы с релятивистской квантовой механикой, а их внимание было сосредоточено на свойствах более лёгких элементов .
Мнение Дирака о роли релятивистских эффектов для квантовой химии оказалось ошибочным по двум причинам:
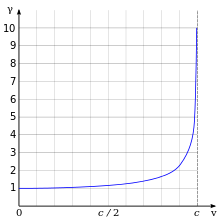
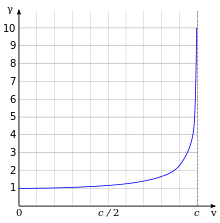
Одним из наиболее важных и известных результатов релятивистской механики является то, что релятивистская масса электрона увеличивается
где — масса покоя электрона , скорость электрона и скорость света соответственно. Рисунок справа иллюстрирует изменение релятивистской массы электрона в зависимости от его скорости. Изменение массы электрона непосредственно влияет на боровский радиус этого электрона
где — приведённая постоянная Планка , а α — постоянная тонкой структуры (релятивистская поправка к модели Бора )
Арнольд Зоммерфельд подсчитал, что для 1s-электрона атома водорода орбитальный радиус 0,0529 нм и α ≈ 1/137 . То есть, такой электрон движется почти с 1/137 скорости света . Можно распространить этот результат на более сложные электронные системы, используя для грубой оценки вклада релятивистских эффектов формулу v ≈ Zc/137 для 1s-электрона, где v является радиальной скоростью этого электрона, Z — заряд ядра (или порядковый номер элемента в таблице Менделеева), а с — скорость света. Например, для золота (Z = 79) получается результат α = 0,58c — то есть он имеет скорость, близкую к 58 % скорости света. Подставляя это в отношение v/c для расчёта релятивистской массы, получаем m rel = 1.22m e . Используя это для оценки боровского радиуса , получаем, что он изменяется на 22 % по сравнению с нерялитивистским радиусом для такого же электрона.
Если подставить в уравнение для релятивистской массы радиус Бора, то можно записать
тогда
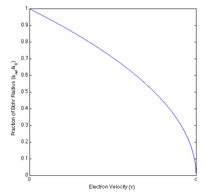
Рисунок справа показывает, как изменяется отношение релятивистского радиуса Бора к нерелятивистскому в зависимости от скорости электрона. Обратите внимание на то, что релятивистская модель предсказывает уменьшение радиуса с увеличением скорости.
Когда боровское описание распространяется на водородоподобные атомы с помощью квантового правила, радиус Бора становится
где — главное квантовое число , а Z — атомный номер. В квантовой механике момент импульса описывается как . Если подставить это в уравнение выше, то для получается выражение
Используя атомную систему единиц , можно упростить выражение
Подставляя это в приведённое выше отношение Бора, получаем
При низком значении и высоком значении будет . Это интуитивно понятно: электроны с более низкими главными квантовыми числами будет иметь более высокую плотность вероятности нахождения у ядра. Ядро с большим зарядом придаёт электронам более высокую скорость ( кулоновское взаимодействие прямо пропорционально величине заряда). Более высокая скорость означает повышенную релятивистскую массу, в результате чего такие электроны будут больше времени находиться вблизи ядра (в квантовой механике полная энергия электрона обратно пропорциональна массе электрона и прямо пропорциональна характерному расстоянию электрона от ядра) и тем самым понижают эффективный радиус орбиталей этих электронов .
Многие из химических и физических различий между 6-м периодом (Cs-Rn) и 5-м периодом (Rb-Xe) возникают из значительных релятивистских эффектов для элементов 6-го периода. Большой заряд ядра и одновременная удаленность электронов от него (на внешних оболочках) заставляет последних двигаться с околосветовыми скоростями. Эти релятивистские эффекты особенно велики для золота, платины и ртути.
Ртуть (Hg) имеет температуру плавления Т пл. = −39 ° C . Связи между атомами ртути Hg-Hg в её кристаллической решётке слабее, чем в простых веществах соседних с ней элементов — кадмия (Т пл. =321 °C) и золота (Т пл. =1064 °C). Лантаноидное сжатие даёт только частичное объяснение этой аномалии. В отличие от многих металлов, в газовой фазе ртуть также обнаруживается в одноатомной форме Hg(g). Также в газовой фазе обнаруживаются и стабильные частицы вида Hg 2 2+ (g). Перечисленные три свойства могут быть объяснены исходя из релятивистских свойств внешних электронных оболочек атомов ртути .
Hg 2 (g) не формируется потому, что 6s 2 -орбиталь сжимается благодаря релятивистскому эффекту и из-за этого мало подходит для образования каких-либо связей с другими атомами; на самом деле Hg-Hg соединение должно быть в основном результатом ван-дер-ваальсовых сил , что объясняет, почему взаимодействие Hg-Hg достаточно слабое, чтобы позволить ртути быть жидкостью при комнатной температуре .
Разница между Au 2 (g) и Hg(g) сходна с разницей между H 2 (g) и He(g). Релятивистское сжатие 6s 2 -орбитали меняет свойства ртути таким образом, что газообразная ртуть может быть названа «псевдо-благородным газом» .
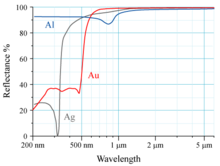
Отражательные свойства Au, Ag, Al показаны на рисунке справа. Человеческий глаз видит электромагнитное излучение с длиной волны около 600 нм как жёлтый свет. Как видно из его спектра отражения, золото кажется жёлтым, так как оно поглощает синий свет больше, чем другие видимые длины волн света. В отражённом свете (который и определяет то, что мы видим) меньше представлена синяя часть оптического спектра .
Поглощение света происходит за счёт электронного перехода 5d --> 6s уровня. Аналогичный переход происходит и в случае Ag, но релятивистские эффекты ниже для Ag. Несмотря на небольшое сжатие 4d- и 5s-орбиталей, расстояние (разница энергий) между ними для Ag по-прежнему намного больше, чем 5d-6s расстояния у Au, так как релятивистские эффекты в последнем случае значительно сильнее. Таким образом, нерелятивистское золото будет белым. Релятивистские эффекты обеспечивают повышение энергии 5d-орбитали и снижение энергии 6s-орбитали .
Аналогичный эффект имеет место для цезия . В то время как другие щелочные металлы серебристо-белые, цезий имеет ярко выраженный золотистый оттенок.
Другие явления, обычно объясняемые с помощью релятивистских эффектов:
С помощью релятивистских эффектов объясняют стабильность анионов «благородных» металлов в таких соединениях, как