Бинарная диаграмма решений (БДР) или "программа с ветвлением" является формой представления булевой функции ${\displaystyle f(x_{1},x_{2},...,x_{n})}$ от ${\displaystyle n}$ переменных в виде направленного ациклического графа , состоящего из внутренних узлов решений (помеченных ${\displaystyle x_{i}}$ ), каждый из которых имеет по два потомка , и двух терминальных узлов (помеченных 0 и 1), каждый из которых соответствует одному из двух значений булевой функции. В зарубежной литературе бинарные диаграммы решений и программы с ветвлением называются binary decision diagram ( BDD ) и branching programs ( BP ) соответственно.

Определение

Булеву функцию ${\displaystyle f(x_{1},x_{2},...,x_{n})}$ можно представить в виде направленного ациклического графа , состоящего из нескольких внутренних узлов решений и двух терминальных узлов, называемых 0-терминальный узел и 1-терминальный узел. Каждый внутренний узел решений на уровне ${\displaystyle i}$ помечен булевой переменной ${\displaystyle x_{i}}$ и имеет по два потомка , называемых младшим потомком и старшим потомком. Переход от внутренного узла ${\displaystyle x_{i}}$ к младшему или старшему потомку выполняется в зависимости от значения переменной ${\displaystyle x_{i}}$ (0 или 1 соответственно). Для заданных значений ${\displaystyle x_{1},x_{2},...,x_{n}}$ путь от корневого узла до 1-терминального узла соответствуют тому, что на этих входных значениях булева функция ${\displaystyle f(x_{1},x_{2},...,x_{n})}$ принимает значение 1.

БДР называется упорядоченной , если различные переменные появляются в одном и том же порядке во всех путях от корневого узла графа до одной из терминальных вершин. При этом, некоторые переменные в путях могут отсутствовать, если над графом ранее была произведена операция сокращения.

БДР называется сокращенной , если для графа применены следующие два правила сокращения:

• Слияние любых изоморфных подграфов.
• Удаление всех узлов с изоморфными потомками.

В большинстве случаев под бинарной диаграммой решений понимают именно сокращенную упорядоченную бинарную диаграмму решений (СУБДР). Преимущество сокращенной упорядоченной БДР в том, что она является канонической (уникальной) для конкретной функции и заданного порядка переменных . Это свойство делает СУБДР полезной для проверки функциональной эквивалентности.

Пример

На рисунке слева изображено бинарное дерево принятия решений (без применения правил сокращения), соответствующее приведенной на этом же рисунке таблице истинности для булевой функции ${\displaystyle f(x_{1},x_{2},x_{3})}$ . Для заданных входных значений ${\displaystyle x_{1}}$ , ${\displaystyle x_{2}}$ , ${\displaystyle x_{3}}$ можно определить значение булевой функции, двигаясь по дереву от корневого узла дерева к терминальным узлам, выбирая направление перехода из узла ${\displaystyle x_{i}}$ в зависимости от входного значения ${\displaystyle x_{i}}$ . Пунктирными линиями на рисунке изображены переходы к младшему потомку, а непрерывными линиями изображены переходы к старшему потомку. Например, если заданы входные значения ( ${\displaystyle x_{1}=0}$ , ${\displaystyle x_{2}=1}$ , ${\displaystyle x_{3}=1}$ ), то из корневого узла ${\displaystyle x_{1}}$ необходимо перейти по пунктирной линии влево (так как значение ${\displaystyle x_{1}}$ равно 0), после этого необходимо перейти по непрерывным линиям вправо (так как значения ${\displaystyle x_{2}}$ и ${\displaystyle x_{3}}$ равны 1). В результате мы окажемся в 1-терминальном узле, то есть значение ${\displaystyle f(x_{1}=0,x_{2}=1,x_{3}=1)}$ равно 1.

Бинарное дерево принятия решений на рисунке слева можно преобразовать в бинарную диаграмму решений путём применения двух правил сокращения. Результирующая БДР изображена на рисунке справа.

История

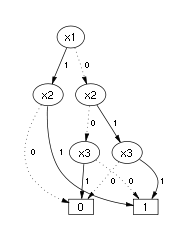
Основной идеей для создания такой структуры данных послужило разложение Шеннона . Любую булеву функцию по одной из входных переменных можно разделить на две подфункции, называемых положительным и отрицательным дополнением, из которых по принципу if-then-else выбирается только одна подфункция в зависимости от значения входной переменной (по которой выполнялось разложение Шеннона). Представляя каждую такую подфункцию в виде поддерева и продолжая разложение по оставшимся входным переменным, можно получить дерево принятия решений , сокращение которого даст бинарную диаграмму решений . Информация об использовании бинарных диаграмм решений или бинарных ветвящихся программ была впервые опубликована в 1959 году в техническом журнале «Bell Systems Technical Journal» . Потенциал для создания эффективных алгоритмов, основанных на использовании этой структуры данных, исследовал из университета Карнеги — Меллон : его подход заключался в использовании фиксированного порядка переменных (для однозначности канонического представления каждой булевой функции) и повторного использования общих подграфов (для компактности). Применение этих двух ключевых концепций позволяет повысить эффективность структур данных и алгоритмов для представления множеств и отношений между ними . Использование несколькими БДР общих подграфов привело к появлению такой структуры данных, как разделяемая сокращенная упорядоченная бинарная диаграмма решений ( Shared Reduced Ordered Binary Decision Diagram ) . Название БДР теперь в основном используется для этой конкретной структуры данных.

Дональд Кнут в своей видеолекции назвал бинарные диаграммы решений « одной из действительно фундаментальных структур данных, которые появились за последние двадцать пять лет » и отметил, что публикация от 1986 года , осветившая использование бинарных диаграмм решений для манипуляции над булевыми функциями, являлась некоторое время наиболее цитируемой публикацией в компьютерной науке.

Применение

БДР широко используются в системах автоматизированного проектирования (САПР) для синтеза логических схем и в формальной верификации .

В электронике каждая конкретная БДР (даже не сокращенная и не упорядоченная) может быть непосредственно реализована заменой каждого узла на мультиплексор с двумя входами и одним выходом.

Порядок переменных

Размер БДР определяется как булевой функцией, так и выбором порядка входных переменных. При составлении графа для булевой функции ${\displaystyle f(x_{1},\ldots ,x_{n})}$ количество узлов в лучшем случае может линейно зависеть от ${\displaystyle n}$ , а в худшем случае зависимость может быть экспоненциальной при неудачном выборе порядка входных переменных. Например, дана булева функция ${\displaystyle f(x_{1},\ldots ,x_{2n})=x_{1}x_{2}+x_{3}x_{4}+\cdots +x_{2n-1}x_{2n}.}$ Если использовать порядок переменных ${\displaystyle x_{1}<x_{3}<\cdots <x_{2n-1}<x_{2}<x_{4}<\cdots <x_{2n}}$ , то понадобится 2 ^{n +1} узлов для представления функции в виде БДР. Иллюстрирующая БДР для функции от 8 переменных изображена на рисунке слева. А если использовать порядок ${\displaystyle x_{1}<x_{2}<x_{3}<x_{4}<\cdots <x_{2n-1}<x_{2n}}$ , то можно получить эквивалентную БДР из 2 n +2 узлов. Иллюстрирующая БДР для функции от 8 переменных изображена на рисунке справа.

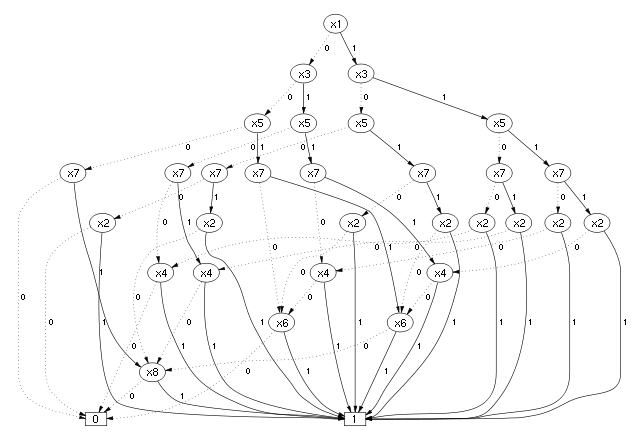
Выбор порядка переменных является критически важным при использовании таких структур данных на практике. Проблема нахождения лучшего порядка переменных является NP-полной задачей . Более того, NP-полной является даже задача нахождения субоптимального порядка переменных, при котором для любой константы c > 1 размер БДР не более чем в c раз больше оптимального . Однако существуют эффективные эвристические методы для решения этой проблемы.

Кроме того, существуют такие функции, для которых размер графа всегда растет экспоненциально с ростом числа переменных, независимо от порядка переменных. Это относится к функциям умножения, что указывает на явную сложность факторизации .

Исследования бинарных диаграмм решений привели к появлению множества смежных видов графов, таких, как BMD ( ), ZDD ( ), FDD ( ), PDD ( ), и MTBDDs (Multiple terminal BDDs).

Логические операции над бинарными диаграммами решений

Многие логические операции ( конъюнкция , дизъюнкция , отрицание ) могут быть выполнены непосредственно над БДР с помощью алгоритмов, выполняющих манипуляции над графами за полиномиальное время. Однако повторение этих операций множество раз, например, при формировании конъюнкций или дизъюнкций набора БДР, могут привести к экспоненциально большой БДР в худшем случае. Это происходит из-за того, что результатом любых предшествующих операций над двумя БДР в общем случае может быть БДР с размером, пропорциональным произведению предшествующих размеров, поэтому для нескольких БДР размер может увеличиваться экспоненциально.

См. также

• Задача выполнимости булевых формул
• Булева алгебра

Примечания

• R. Ubar, «Test Generation for Digital Circuits Using Alternative Graphs (in Russian)», in Proc. Tallinn Technical University, 1976, No.409, Tallinn Technical University, Tallinn, Estonia, pp. 75–81.

Рекомендуемая литература

• D. E. Knuth, «The Art of Computer Programming Volume 4, Fascicle 1: Bitwise tricks & techniques; Binary Decision Diagrams» (Addison-Wesley Professional, March 27, 2009) viii+260pp, ISBN 0-321-58050-8 . available for download.
• H. R. Andersen « », Lecture Notes, 1999, IT University of Copenhagen.
• Ch. Meinel, T. Theobald, « , Springer-Verlag, Berlin, Heidelberg, New York, 1998. Complete textbook available for download.
• Rüdiger Ebendt; Görschwin Fey; Rolf Drechsler. Advanced BDD optimization (англ.) . — (англ.) ( , 2005. — ISBN 978-0-387-25453-1 .
• Bernd Becker; Rolf Drechsler. Binary Decision Diagrams: Theory and Implementation (англ.) . — (англ.) ( , 1998. — ISBN 978-1-4419-5047-5 .
• O. A. Finko, K. S. Meretukov, , OP&PM Surveys on Applied and Industrial Mathematics. Proceedings II International Baltic Symposium on Applied and Industrial Mathematics (Svetlogorsk, June 12 – 18, 2016), 23, TVP, Moscow, 2016, 167-168.

Ссылки

• : The ABCD package by Armin Biere, Johannes Kepler Universität, Linz.
• , BDD package, Carnegie Mellon University, Pittsburgh
• : BDD package, University of Colorado, Boulder
• : multi-platform academic BDD package, University of Maribor, Slovenia
• , a Java port of BuDDy that also interfaces to CUDD, CAL, and JDD
• The Berkeley package which does breadth-first manipulation
• A. Costa , includes a BDD boolean logic simplifier supporting up to 32 inputs / 32 outputs (independently)
• : A C++ library with support for integer valued and hierarchical decision diagrams.
• : A C++ library developed at University of Bonn, Germany, supporting several BDD variants and multi-threading.