В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия , с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании .

Формальная логика

Логические операции с понятиями — такие мыслительные действия, результатом которых являются понимание смысла либо изменение содержания или объёма понятий, а также образование новых понятий .

Операция, раскрывающая сущность понятия:

• определение ;

К операциям, которые связаны преимущественно с изменением содержания понятий, относятся:

• отрицание (NOT);
• ограничение ;
• обобщение ;

К операциям, которые связаны преимущественно с изменением объёмов понятий, относятся:

• логическое сложение (OR);
• логическое умножение (AND);
• логическое вычитание (XOR);
• логическое деление .

Данные операции могут быть записаны математически с помощью теории множеств .

Переход же к математической логике связан с понятием суждений и установлением операций над ними с целью получения сложных суждений.

Математическая логика

Логическая операция ( логический оператор , логическая связка , пропозициональная связка ) — операция над высказываниями , позволяющая составлять новые высказывания путём соединения более простых .

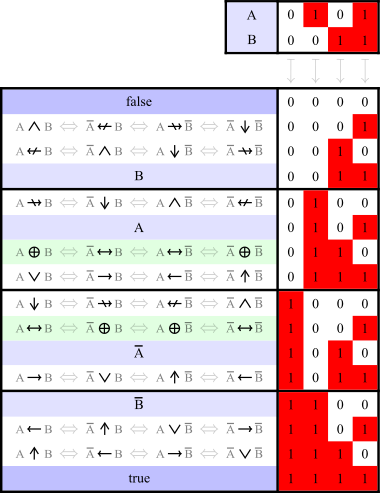
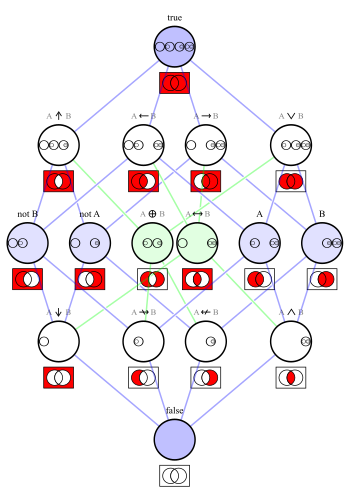
В качестве основных обычно называют конъюнкцию ( ${\displaystyle \land }$ или &), дизъюнкцию ( ${\displaystyle \lor }$ ), импликацию ( ${\displaystyle \to }$ ), отрицание ( ${\displaystyle \neg }$ ). В смысле классической логики логические связки могут быть определены через алгебру логики . В асинхронной секвенциальной логике определена логико-динамическая связка в виде операции венъюнкции ( ${\displaystyle \angle }$ ).

Программирование

Логическая операция — в программировании операция над выражениями логического (булевского) типа , соответствующая некоторой операции над высказываниями в алгебре логики . Как и высказывания, логические выражения могут принимать одно из двух истинностных значений — «истинно» или «ложно». Логические операции служат для получения сложных логических выражений из более простых. В свою очередь, логические выражения обычно используются как условия для управления последовательностью выполнения программы.

В некоторых языках программирования (например, в языке C++ или Си ) вместо логического типа или одновременно с ним используются числовые типы . В этом случае считается, что отличное от нуля значение соответствует логической истине, а ноль — логической лжи.

Значение отдельного бита также можно рассматривать как логическое, если считать, что 1 означает «истинно», а 0 — «ложно». Это позволяет применять логические операции к отдельным битам, к битовым векторам покомпонентно и к числам в двоичном представлении поразрядно. Такое одновременное применение логической операции к последовательности битов осуществляется с помощью побитовых логических операций . Побитовые логические операции используются для оперирования отдельными битами или группами битов, применяются для наложения битовых масок, выполнения различных арифметических вычислений.

Среди логических операций наиболее известны конъюнкция (&&), дизъюнкция (||), отрицание (!). Их нередко путают с битовыми операциями, хотя это разные вещи. Например, следующий код на языке Си :

if (action_required && some_condition()) 
{
    /* какие-то действия */
}

не выполнит вызов подпрограммы some_condition() , если значение логической переменной action_required ложно. При такой операции второй аргумент операции «&&» вообще не будет вычислен.

В языках программирования

В следующей таблице для некоторых языков программирования приведены встроенные операторы и функции, реализующие логические операции.

(file)		(file)

См. также

• Логическая константа
• Логический элемент
• Комбинационная логика
• Логическое выражение
• Логический вывод
• Секвенциальная логика
• Умозаключение

Примечания

Ссылки

• БСЭ. Логическая операция (в программировании) // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров . — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
• БСЭ. Логические операции (в логике) // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров . — 3-е изд. — М. : Советская энциклопедия, 1969—1978.