Ме́тод Га́усса в небесной механике и астродинамике используется для первоначального определения параметров орбиты небесного тела по трём наблюдениям.

На практике для увеличения точности используется больше наблюдений, но в теории достаточно трёх. Кроме небесных координат объекта, необходимыми сведениями являются моменты наблюдений и земные координаты пунктов наблюдения.

История

В 1801 году была открыта Церера , но в течение некоторого времени её наблюдения были затруднены из-за близости к Солнцу, после чего было трудно снова найти её на небе. Карл Фридрих Гаусс поставил себе задачу определения её орбиты по имевшимся наблюдениям, за счёт чего и приобрёл мировую известность . Однако описанный ниже метод годится только для определения орбит с фокусом в теле, с которого ведутся наблюдения, так что задача Гаусса была сложнее.

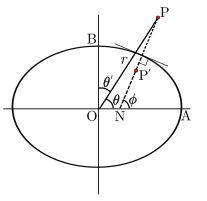
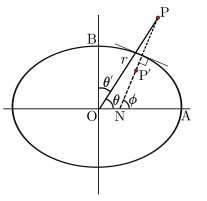
Вектор положения наблюдателя

Вектор положения наблюдателя (в экваториальной системе координат ) можно вычислить, зная широту места наблюдения и местное звёздное время :

${\displaystyle \mathbf {R_{n}} =\left[{R_{e} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\cos \phi _{n}(\cos \theta _{n}\ \mathbf {\hat {I}} +\sin \theta _{n}\ \mathbf {\hat {J}} )+\left[{R_{e}(1-f)^{2} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\sin \phi _{n}\ \mathbf {\hat {K}} }$

или:

${\displaystyle \mathbf {R_{n}} =R_{e}\cos \phi '_{n}\cos \theta _{n}\ \mathbf {\hat {I}} +R_{e}\cos \phi '_{n}\sin \theta _{n}\ \mathbf {\hat {J}} +R_{e}\sin \phi '_{n}\ \mathbf {\hat {K}} ,}$

где:

• ${\displaystyle \mathbf {R_{n}} }$ — вектор положения наблюдателя;
• ${\displaystyle R_{e}}$ — экваториальный радиус тела, на котором находится наблюдатель;
• ${\displaystyle f}$ — сплюснутость тела у полюсов (например, для Земли — 0.003353);
• ${\displaystyle \phi _{n}}$ — геодезическая широта;
• ${\displaystyle \phi '_{n}}$ — геоцентрическая широта;
• ${\displaystyle H_{n}}$ — высота;
• ${\displaystyle \theta _{n}}$ — местное звёздное время.

Вектор направления на объект

Вектор направления на объект может быть вычислен с помощью склонения и прямого восхождения :

${\displaystyle \mathbf {{\hat {\rho }}_{n}} =\cos \delta _{n}\cos \alpha _{n}\ \mathbf {\hat {I}} +\cos \delta _{n}\sin \alpha _{n}\ \mathbf {\hat {J}} +\sin \delta _{n}\ \mathbf {\hat {K}} }$ ,

где:

• ${\displaystyle \mathbf {{\hat {\rho }}_{n}} }$ — единичный вектор направления на объект;
• ${\displaystyle \delta _{n}}$ — склонение;
• ${\displaystyle \alpha _{n}}$ — прямое восхождение.

Определение орбиты

Далее нужно получить вектор расстояния до объекта, а не только единичный вектор направления на него.

Шаг 1

Вычисляются интервалы между наблюдениями:

${\displaystyle \tau _{1}=t_{1}-t_{2}}$

${\displaystyle \tau _{3}=t_{3}-t_{2}}$

${\displaystyle \tau =t_{3}-t_{1},}$

где ${\displaystyle t_{n}}$ — моменты наблюдений.

Шаг 2

Вычисляются векторные произведения :

${\displaystyle \mathbf {p_{1}} =\mathbf {{\hat {\rho }}_{2}} \times \mathbf {{\hat {\rho }}_{3}} }$

${\displaystyle \mathbf {p_{2}} =\mathbf {{\hat {\rho }}_{1}} \times \mathbf {{\hat {\rho }}_{3}} }$

${\displaystyle \mathbf {p_{3}} =\mathbf {{\hat {\rho }}_{1}} \times \mathbf {{\hat {\rho }}_{2}} }$

Шаг 3

Вычисляются смешанные произведения :

${\displaystyle D_{0}=\mathbf {{\hat {\rho }}_{1}} \cdot \mathbf {p_{1}} =\mathbf {{\hat {\rho }}_{1}} \cdot (\mathbf {{\hat {\rho }}_{2}} \times \mathbf {{\hat {\rho }}_{3}} )}$

${\displaystyle D_{11}=\mathbf {R_{1}} \cdot \mathbf {p_{1}} \qquad D_{12}=\mathbf {R_{1}} \cdot \mathbf {p_{2}} \qquad D_{13}=\mathbf {R_{1}} \cdot \mathbf {p_{3}} }$

${\displaystyle D_{21}=\mathbf {R_{2}} \cdot \mathbf {p_{1}} \qquad D_{22}=\mathbf {R_{2}} \cdot \mathbf {p_{2}} \qquad D_{23}=\mathbf {R_{2}} \cdot \mathbf {p_{3}} }$

${\displaystyle D_{31}=\mathbf {R_{3}} \cdot \mathbf {p_{1}} \qquad D_{32}=\mathbf {R_{3}} \cdot \mathbf {p_{2}} \qquad D_{33}=\mathbf {R_{3}} \cdot \mathbf {p_{3}} }$

Шаг 4

Вычисляются позиционные коэффициенты:

${\displaystyle A={\frac {1}{D_{0}}}\left(-D_{12}{\frac {\tau _{3}}{\tau }}+D_{22}+D_{32}{\frac {\tau _{1}}{\tau }}\right)}$

${\displaystyle B={\frac {1}{6D_{0}}}\left[D_{12}\left(\tau _{3}^{2}-\tau ^{2}\right){\frac {\tau _{3}}{\tau }}+D_{32}\left(\tau ^{2}-\tau _{1}^{2}\right){\frac {\tau _{1}}{\tau }}\right]}$

${\displaystyle E=\mathbf {R_{2}} \cdot \mathbf {{\hat {\rho }}_{2}} }$

Шаг 5

Вычисляется модуль вектора положения наблюдателя в момент второго наблюдения:

${\displaystyle {R_{2}}^{2}=\mathbf {R_{2}} \cdot \mathbf {R_{2}} }$

Шаг 6

Вычисляются коэффициенты полинома для поиска расстояния:

${\displaystyle a=-\left(A^{2}+2AE+{R_{2}}^{2}\right)}$

${\displaystyle b=-2\mu B(A+E)}$

${\displaystyle c=-\mu ^{2}B^{2},}$

где ${\displaystyle \mu }$ — гравитационный параметр тела, вокруг которого происходит вращение.

Шаг 7

Ищутся решения уравнения:

${\displaystyle {r_{2}}^{8}+a{r_{2}}^{6}+b{r_{2}}^{3}+c=0,}$

где ${\displaystyle r_{2}}$ — расстояние до объекта в момент второго наблюдения.

У кубического уравнения может быть до трёх действительных корней. В случае, если их больше одного, необходимо проверить каждый из них.

Шаг 8

Вычисляются расстояния от точек наблюдения до объекта в каждый из моментов наблюдений:

${\displaystyle \rho _{1}={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{31}{\dfrac {\tau _{1}}{\tau _{3}}}+D_{21}{\dfrac {\tau }{\tau _{3}}}\right){r_{2}}^{3}+\mu D_{31}\left(\tau ^{2}-{\tau _{1}}^{2}\right){\dfrac {\tau _{1}}{\tau _{3}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{3}}^{2}\right)}}-D_{11}\right]}$

${\displaystyle \rho _{2}=A+{\frac {\mu B}{{r_{2}}^{3}}}}$

${\displaystyle \rho _{3}={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{13}{\dfrac {\tau _{3}}{\tau _{1}}}-D_{23}{\dfrac {\tau }{\tau _{1}}}\right){r_{2}}^{3}+\mu D_{13}\left(\tau ^{2}-{\tau _{3}}^{2}\right){\dfrac {\tau _{3}}{\tau _{1}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{1}}^{2}\right)}}-D_{33}\right]}$

Шаг 9

Вычисляются позиционные вектора объекта (в экваториальной системе координат ):

${\displaystyle \mathbf {r_{1}} =\mathbf {R_{1}} +\rho _{1}\mathbf {{\hat {\rho }}_{1}} }$

${\displaystyle \mathbf {r_{2}} =\mathbf {R_{2}} +\rho _{2}\mathbf {{\hat {\rho }}_{2}} }$

${\displaystyle \mathbf {r_{3}} =\mathbf {R_{3}} +\rho _{3}\mathbf {{\hat {\rho }}_{3}} }$

Шаг 10

Вычисляются коэффициенты Лагранжа . Из-за этого пункта определение орбит становится неточным:

${\displaystyle f_{1}\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{2}}$

${\displaystyle f_{3}\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{2}}$

${\displaystyle g_{1}\approx \tau _{1}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{3}}$

${\displaystyle g_{3}\approx \tau _{3}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{3}}$

Шаг 11

Вычисляется вектор скорости объекта в момент второго наблюдения (в экваториальной системе координат):

${\displaystyle \mathbf {v_{2}} ={\frac {1}{f_{1}g_{3}-f_{3}g_{1}}}\left(-f_{3}\mathbf {r_{1}} +f_{1}\mathbf {r_{3}} \right)}$

Шаг 12

Теперь известно положение и скорость объекта в один момент времени. Значит, возможно определить параметры орбиты .

Примечания

Литература

• Der, Gim J.. «New Angles-only Algorithms for Initial Orbit Determination.» Advanced Maui Optical and Space Surveillance Technologies Conference. (2012). Print (англ.)