Interested Article - Кривая Лоренца
- 2020-01-06
- 2
Кривая Лоренца ( англ. Lorenz curve ) — графическое изображение функции распределения , предложенная американским экономистом Максом Отто Лоренцем в 1905 году как показатель неравенства в доходах населения . Кривая Лоренца представляет функцию распределения, в которой аккумулируются доли численности и доходов населения. В прямоугольной системе координат кривая Лоренца является выпуклой вниз и проходит под диагональю единичного квадрата , расположенного в I координатной четверти .
Определение
Согласно американским экономистам К. Р. Макконнеллу и С. Л. Брю кривая Лоренца — это кривая распределения дохода в экономике, где суммарный процент домохозяйств, получающий доход, отложен на оси абсцисс , а суммарный процент доходов — по оси ординат . Кривая Лоренца демонстрирует степень неравенства распределения доходов: область между линией абсолютного равенства и кривой Лоренца (практического распределения дохода) .
Каждая точка на кривой Лоренца соответствует утверждению вроде «20 самых бедных процентов населения получают всего 7 % дохода». В случае равного распределения каждая группа населения имеет доход, пропорциональный своей численности. Такой случай описывается кривой равенства ( line of perfect equality ), являющейся прямой, соединяющей начало координат и точку (1;1). В случае полного неравенства (когда лишь один член общества имеет доход) кривая ( line of perfect inequality ) сначала «прилипает» к оси абсцисс, а потом из точки (1;0) «взмывает» к точке (1;1). Кривая Лоренца заключена между кривыми равенства и полного неравенства .
Кривые Лоренца применяют для распределений не только доходов, но и имущества домохозяйств, долей рынка для фирм в отрасли, природных ресурсов по государствам.
Формула
Формально, если — это доля населения с подушевым доходом не более , т.е. функция распределения для дохода, то средний доход на душу населения можно вычислить по формуле
где есть плотность распределения для , если она существует. Если то функция Лоренца определяется формулой
(при или функция Лоренца не определена). График функции Лоренца называется кривой Лоренца . Если существует обратная функция , то
Пример . Если при и при , то . При функция распределения стремится к функции скачка в точке 1, отвечающей равномерному распределению дохода, а , то есть кривая Лоренца стремится к кривой равенства.
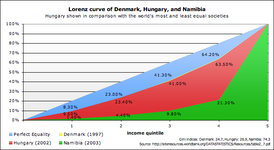
Присутствие точки на кривой Лоренца означает, что доля самых бедных жителей совокупно обладает долей общего дохода. Например, на приведенном ниже рисунке видно, что на примерно 3/4 самых бедных жителей приходится примерно половина всех доходов.
Производные показатели неравенства
Из кривой Лоренца можно вывести количественные показатели неравенства, например, коэффициент Джини и индекс Робин Гуда.

Индекс Робин Гуда (Robin Hood index), также известный как индекс Гувера (Hoover index), — это ещё один показатель неравенства по доходам, имеющий связь с кривой Лоренца. Он равен той доле дохода общества, которую необходимо перераспределить для достижения равенства. Графически он представим как самый длинный вертикальный отрезок, соединяющий фактическую кривую Лоренца с линией равенства (биссектрисой I координатной четверти).
При абсолютной делимости дохода индекс Гувера принадлежит полуоткрытому интервалу [0;1). Если же доход не делим до бесконечности, то говорят о доле дохода, перераспределение которой максимально приближает данное общество к равенству.
Индекс Робин Гуда широко используется в оценках обеспеченности населённых районов врачами общей практики. При таких оценках кривая Лоренца будет наполняться не доходами, а удельным числом врачей общей практики на местность или группу людей, а ранжировать по данному показателю следует не домохозяйства, а местности или группы людей. Таким образом, он показывает, какую часть докторов следует перенаправить в другие районы для поддержания равной обеспеченности медицинским персоналом на всей исследуемой территории.
Примечания
- Макконнелл К. Р. , Брю С. Л. Экономикс: принципы, проблемы и политика : [ рус. ] = Economics: Principles, Problems, and Policies. — М. : Республика , 1992. — Т. 2. — ISBN 5-250-01486-0 .
- 2020-01-06
- 2















































