Грамматика эсперанто
- 1 year ago
- 0
- 0
В информатике неоднозначной грамматикой называется формальная грамматика , которая может породить некоторую строку более чем одним способом (то есть для строки есть более одного дерева разбора). Язык называется существенно неоднозначным , если он может быть порождён только неоднозначными грамматиками.
Грамматики некоторых языков программирования неоднозначны. При разборе таких языков необходимо учитывать семантическую информацию для выбора правильного варианта. Например, на языке C следующая запись:
x * y;
может быть проинтерпретирована как либо:
y
с типом
указатель
-на-
x
, или
x
умножается на
y
, а результат игнорируется.
Чтобы выбрать между этими интерпретациями,
компилятор
должен обратиться к своей таблице символов, чтобы узнать, было ли объявление
x
в качестве имени typedef в данной области видимости.
Контекстно свободная грамматика
является неоднозначной, так как есть два левосторонних вывода для строки a + a + a:
| A | → A + A | A | → A + A | ||
| → a + A | → A + A + A | ||||
| → a + A + A | → a + A + A | ||||
| → a + a + A | → a + a + A | ||||
| → a + a + a | → a + a + a |
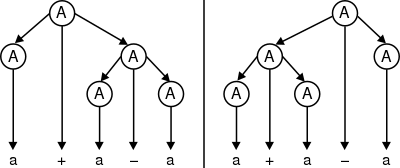
Также, грамматика является неоднозначной, поскольку есть два дерева разбора для строки a + a − a:
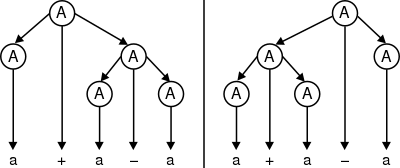
Однако, язык, который она порождает, не является существенно неоднозначным, поскольку следующая однозначная грамматика порождает этот же язык:
Общая задача определения, является ли грамматика неоднозначной, алгоритмически неразрешима . Не может существовать алгоритма, определяющего неоднозначность грамматики, поскольку неразрешимая задача соответствия Поста сводится к задаче неоднозначности.
Существует очевидная трудность в синтаксическом анализе неоднозначной грамматики детерминированным анализатором , но недетерминированный анализ приводит к значительному проигрышу в эффективности. Большинство конструкций, требующих синтаксического анализа, могут быть распознаны однозначными грамматиками. Некоторые неоднозначные грамматики могут быть преобразованы в однозначные, но общей процедуры для этого преобразования нет, так же как нет и алгоритма определения неоднозначности грамматики. Генераторы компиляторов , такие как , способны устранять некоторые виды неоднозначности, например используя ограничения приоритета и ассоциативности .
В то время как некоторые языки (множества строк, порождаемых грамматикой) имеют как однозначные, так и неоднозначные грамматики, существуют языки, для которых не существует однозначной грамматики. Примером существенно неоднозначного языка является объединение и . Это контекстно-свободный язык как объединение контекстно-свободных языков, но Введение в теорию автоматов… содержит доказательство того, что нет возможности однозначно разобрать строки в (не контекстно-свободном) подмножестве , являющемся пересечением этих двух языков.