Тригонометрический
ряд Фурье
— представление произвольной функции
 с периодом
с периодом
 в виде ряда
в виде ряда
-

|
(1)
|
или с использованием комплексной записи, в виде ряда:
-
 .
.
Скалярное произведение и ортогональность
Пусть
 ,
,
 — две функции
пространства
— две функции
пространства
![L^2\left[-\frac{\tau}{2},\frac{\tau}{2}\right]](/images/005/334/5334584/7.jpg?rand=677991) . Определим их скалярное произведение
. Определим их скалярное произведение
-

Условие ортогональности
-

где
 —
символ Кронекера
. Таким образом, скалярное произведение
ортогональных
функций равно квадрату
нормы функции
при
—
символ Кронекера
. Таким образом, скалярное произведение
ортогональных
функций равно квадрату
нормы функции
при
 или нулю в противном случае.
или нулю в противном случае.
Следующее наблюдение является ключевым в теории рядов Фурье: функции вида
 ,
,
 попарно ортогональны относительно этого скалярного произведения, то есть при всех целых неотрицательных
попарно ортогональны относительно этого скалярного произведения, то есть при всех целых неотрицательных
 :
:
-

и при всех целых неотрицательных
 ,
,

-
 .
.
Ещё одно важное свойство состоит в том, что тригонометрическая система функций является
базисом
в
пространстве
![L^2[0,2\pi]](/images/005/334/5334584/19.jpg?rand=62518) . Иными словами, если некоторая функция из этого пространства ортогональна всем функциям вида
. Иными словами, если некоторая функция из этого пространства ортогональна всем функциям вида
 , то она тождественно равна нулю (если точнее, то равна нулю
почти всюду
).
, то она тождественно равна нулю (если точнее, то равна нулю
почти всюду
).
Классическое определение
Тригонометрическим рядом Фурье
функции
![f\in L_2([-\pi,\pi])](/images/005/334/5334584/21.jpg?rand=384519) называют
функциональный ряд
вида
называют
функциональный ряд
вида
-

|
(1)
|
где
-

-

-

Числа
 ,
,
 и
и
 (
(
 ) называются
коэффициентами Фурье функции
) называются
коэффициентами Фурье функции
 . Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию
. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию
![f\in L_2([-\pi,\pi])](/images/005/334/5334584/31.jpg?rand=74643) в виде ряда (1), и нам надо определить неизвестные коэффициенты
в виде ряда (1), и нам надо определить неизвестные коэффициенты
 ,
,
 и
и
 . Если умножить правую часть (1) на
. Если умножить правую часть (1) на
 и проинтегрировать по промежутку
и проинтегрировать по промежутку
![[-\pi,\pi]](/images/005/334/5334584/36.jpg?rand=756077) , благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент
, благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент
 . Аналогично для
. Аналогично для

Ряд (1)
сходится
к функции
 в пространстве
в пространстве
![L_2([-\pi,\pi])](/images/005/334/5334584/40.jpg?rand=945146) . Иными словами, если обозначить через
. Иными словами, если обозначить через
 частичные суммы ряда (1):
частичные суммы ряда (1):
-
 ,
,
то их
среднеквадратичное отклонение
от функции
 будет стремиться к нулю:
будет стремиться к нулю:
-
 .
.
Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно(см.ниже).
Комплексная запись
Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем
пространство
![L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/45.jpg?rand=505139) комплекснозначных функций со
скалярным произведением
комплекснозначных функций со
скалярным произведением
-
 .
.
Мы также рассматриваем систему функций
-
-
 .
.
Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция
![f\in L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/48.jpg?rand=737589) может быть разложена по ним в ряд Фурье:
может быть разложена по ним в ряд Фурье:
-
 ,
,
где ряд в правой части сходится к
 по норме в
по норме в
![f\in L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/51.jpg?rand=419327) . Здесь
. Здесь
-
 .
.
Коэффициенты :
 связаны с классическими коэффициентами Фурье по следующим формулам:
связаны с классическими коэффициентами Фурье по следующим формулам:
-

-

-

-

-

-
Комплексная функция вещественной переменной раскладывается в такой же ряд Фурье по мнимым экспонентам, как и вещественная, но, в отличие от последней, для её разложения
 и
и
 не будут, вообще говоря, комплексно сопряженными.
не будут, вообще говоря, комплексно сопряженными.
Свойства тригонометрического ряда Фурье
Все утверждения этого параграфа верны в предположении, что участвующие в них функции (и результаты операций с ними) лежат в
пространстве
![L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/61.jpg?rand=961637) .
.
-
Вычисление коэффициентов Фурье является линейной операцией:
-

-
Справедливо
равенство Парсеваля
:
-
-
 .
.
-
Коэффициенты Фурье производной легко выражаются через коэффициенты Фурье самой функции:
-

-
коэффициенты Фурье произведения двух функций выражаются
свёрткой
коэффициентов Фурье сомножителей:
-

-
рассмотрим операцию
свертки
функций:
-

где функции предполагаются периодически продолженными с промежутка
![[-\pi,\pi]](/images/005/334/5334584/67.jpg?rand=83324) на всю прямую. Тогда
на всю прямую. Тогда
-

Разложения некоторых функций в ряд Фурье
|
Функция
|
Ряд Фурье
|
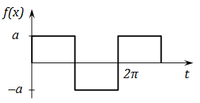
|

|

|

|
См. также
Примечания
Литература
-
Жук В.В., Натансон Г.И.
Тригонометрические ряды Фурье и элементы теории аппроксимации. —
Л.
: Изд-во Ленингр. ун-та, 1983. — С. 188.
-
Рудин У.
Основы математического анализа. — 1976.
-
Пискунов Н. С.
Дифференциальное и интегральное исчисления для ВТУЗов. —
М.
: «Наука», 1964. — Т. 2.









![L^2\left[-\frac{\tau}{2},\frac{\tau}{2}\right]](/images/005/334/5334584/7.jpg?rand=677991)











![L^2[0,2\pi]](/images/005/334/5334584/19.jpg?rand=62518)

![f\in L_2([-\pi,\pi])](/images/005/334/5334584/21.jpg?rand=384519)









![f\in L_2([-\pi,\pi])](/images/005/334/5334584/31.jpg?rand=74643)




![[-\pi,\pi]](/images/005/334/5334584/36.jpg?rand=756077)



![L_2([-\pi,\pi])](/images/005/334/5334584/40.jpg?rand=945146)




![L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/45.jpg?rand=505139)


![f\in L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/48.jpg?rand=737589)


![f\in L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/51.jpg?rand=419327)









![L^2([-\pi,\pi],\mathbb{C})](/images/005/334/5334584/61.jpg?rand=961637)





![[-\pi,\pi]](/images/005/334/5334584/67.jpg?rand=83324)


























