А́лгебра Кэ́ли
— система
гиперкомплексных чисел
, 8-
мерная
алгебра над полем
вещественных чисел
.
Обычно обозначается
O
{\displaystyle \mathbb {O} }
, поскольку её элементы (
числа Кэли
) называются иногда
октонионами
или
октавами
.
Впервые рассмотрена в
1843 году
, приятелем
Уильяма Гамильтона
, а двумя годами позже — независимо
Артуром Кэли
.
Число Кэли — это
линейная комбинация
элементов
{
1
,
i
,
j
,
k
,
l
,
i
l
,
j
l
,
k
l
}
{\displaystyle \{1,i,j,k,l,il,jl,kl\}}
.
Каждая октава
x
{\displaystyle x}
может быть записана в форме:
x
=
x
0
+
x
1
i
+
x
2
j
+
x
3
k
+
x
4
l
+
x
5
i
l
+
x
6
j
l
+
x
7
k
l
{\displaystyle x=x_{0}+x_{1}\,i+x_{2}\,j+x_{3}\,k+x_{4}\,l+x_{5}\,il+x_{6}\,jl+x_{7}\,kl}
с вещественными коэффициентами
x
i
{\displaystyle x_{i}}
. Октонионы находят применение в физике, в частности, в
специальной теории относительности
и
теории струн
.
Таблицы умножения
Таблица умножения
элементов октавы:
1
i
(
e1
)
j
(
e2
)
k
(
e3
)
l
(
e4
)
il
(
e5
)
jl
(
e6
)
kl
(
e7
)
i
(
e1
)
−1
k
−
j
il
−
l
−
kl
jl
j
(
e2
)
−
k
−1
i
jl
kl
−
l
−
il
k
(
e3
)
j
−
i
−1
kl
−
jl
il
−
l
l
(
e4
)
−
il
−
jl
−
kl
−1
i
j
k
il
(
e5
)
l
−
kl
jl
−
i
−1
−
k
j
jl
(
e6
)
kl
l
−
il
−
j
k
−1
−
i
kl
(
e7
)
−
jl
il
l
−
k
−
j
i
−1
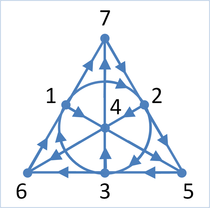
Плоскость Фано
для
мнемонического
запоминания таблицы умножения
Таблица (Кэли) умножения октонионов
:
e
0
e
1
e
2
e
3
e
4
e
5
e
6
e
7
e
1
−1
e
3
−e
2
e
5
−e
4
−e
7
e
6
e
2
−e
3
−1
e
1
e
6
e
7
−e
4
−e
5
e
3
e
2
−e
1
−1
e
7
−e
6
e
5
−e
4
e
4
−e
5
−e
6
−e
7
−1
e
1
e
2
e
3
e
5
e
4
−e
7
e
6
−e
1
−1
−e
3
e
2
e
6
e
7
e
4
−e
5
−e
2
e
3
−1
−e
1
e
7
−e
6
e
5
e
4
−e
3
−e
2
e
1
−1
Иногда заменяются буквенным обозначением:
Номер
1
2
3
4
5
6
7
Буквы
i
j
k
l
il
jl
kl
Замена
i
j
k
l
m
n
o
Свойства
По
теореме Фробениуса
алгебра Кэли является единственной 8-мерной вещественной
альтернативной алгеброй
без
делителей нуля
.
Алгебра Кэли является алгеброй с однозначным делением и с единицей, альтернативной, но
неассоциативной
и
некоммутативной
.
Для октониона
x
=
x
0
+
x
1
i
+
x
2
j
+
x
3
k
+
x
4
l
+
x
5
i
l
+
x
6
j
l
+
x
7
k
l
{\displaystyle x=x_{0}+x_{1}\,i+x_{2}\,j+x_{3}\,k+x_{4}\,l+x_{5}\,il+x_{6}\,jl+x_{7}\,kl}
операция
определена равенством:
x
∗
=
x
0
−
x
1
i
−
x
2
j
−
x
3
k
−
x
4
l
−
x
5
i
l
−
x
6
j
l
−
x
7
k
l
{\displaystyle x^{*}=x_{0}-x_{1}\,i-x_{2}\,j-x_{3}\,k-x_{4}\,l-x_{5}\,il-x_{6}\,jl-x_{7}\,kl}
.
Сопряжение удовлетворяет равенствам:
(
x
y
)
∗
=
y
∗
x
∗
{\displaystyle (xy)^{*}=y^{*}x^{*}}
и
x
∗
=
−
1
6
(
x
+
(
i
x
)
i
+
(
j
x
)
j
+
(
k
x
)
k
+
(
l
x
)
l
+
(
(
i
l
)
x
)
(
i
l
)
+
(
(
j
l
)
x
)
(
j
l
)
+
(
(
k
l
)
x
)
(
k
l
)
)
.
{\displaystyle x^{*}=-{\frac {1}{6}}(x+(ix)i+(jx)j+(kx)k+(lx)l+((il)x)(il)+((jl)x)(jl)+((kl)x)(kl)).}
Вещественная часть октониона
x
{\displaystyle x}
определена равенством:
1
2
(
x
+
x
∗
)
=
x
0
{\displaystyle {\frac {1}{2}}(x+x^{*})=x_{0}}
,
мнимая часть:
1
2
(
x
−
x
∗
)
{\displaystyle {\frac {1}{2}}(x-x^{*})}
.
Норма
октониона
x
{\displaystyle x}
:
‖
x
‖
=
x
∗
x
{\displaystyle \|x\|={\sqrt {x^{*}x}}}
;
‖
x
‖
=
0
{\displaystyle \|x\|=0}
тогда и только тогда, когда
x
=
0
{\displaystyle x=0}
. Из определения нормы следует, что октонион
x
≠
0
{\displaystyle x\neq 0}
обратим и
x
−
1
=
x
∗
‖
x
‖
2
{\displaystyle x^{-1}={\frac {x^{*}}{\|x\|^{2}}}}
.
Из-за неассоциативности октонионы не имеют матричных представлений.
Примечания
(неопр.)
(HTML) (26 января 2003). Дата обращения: 4 октября 2009. Архивировано из
27 февраля 2012 года.
от 5 мая 2010 на
Wayback Machine
(недоступная ссылка с 19-05-2013 [3893 дня] —
)
(англ.)
. Ссылка недоступна по состоянию на 6 ноября 2010.
(недоступная ссылка)
на yahoo.com,
от 6 мая 2010 на
Wayback Machine
на scientific.ru.
Антисимметрия по диагонали для −1
Литература
Джон Баэс
.
от 4 марта 2016 на
Wayback Machine
// Гиперкомплексные числа в геометрии и физике, № 1(5), Vol 3(2006), с.120-176.
Счётные множества
Вещественные числа и их расширения
Инструменты расширения числовых систем
Другие числовые системы
См. также
Размерность — степень 2
Комплексные числа
C
{\displaystyle \mathbb {C} }
(разм. 2)
Кватернионы
H
{\displaystyle \mathbb {H} }
(разм. 4)
O
{\displaystyle \mathbb {O} }
(разм. 8)
Седенионы
S
{\displaystyle \mathbb {S} }
(разм. 16)
См. также