MD4 ( Message Digest 4 ) — криптографическая хеш-функция , разработанная профессором Массачусетского университета Рональдом Ривестом в 1990 году, и впервые описанная в . Для произвольного входного сообщения функция генерирует 128-разрядное хеш-значение, называемое дайджестом сообщения. Этот алгоритм используется в протоколе аутентификации MS-CHAP , разработанном корпорацией Майкрософт для выполнения процедур проверки подлинности удаленных рабочих станций Windows . Является предшественником MD5 .

Алгоритм MD4

Предполагается, что на вход подано сообщение, состоящее из ${\displaystyle b}$ бит, хеш которого нам предстоит вычислить. Здесь ${\displaystyle b}$ — произвольное неотрицательное целое число ; оно может быть нулём, не обязано быть кратным восьми, и может быть сколь угодно большим. Запишем сообщение побитно, в виде:

  ${\displaystyle m_{0}m_{1}\ldots m_{b-1}}$

Ниже приведены 5 шагов, используемые для вычисления хеша сообщения.

Шаг 1. Добавление недостающих битов.

Сообщение расширяется так, чтобы его длина в битах по модулю 512 равнялась 448. Таким образом, в результате расширения, сообщению недостает 64 бита до длины, кратной 512 битам. Расширение производится всегда, даже если сообщение изначально имеет нужную длину.

Расширение производится следующим образом: один бит, равный 1, добавляется к сообщению, а затем добавляются биты, равные 0, до тех пор, пока длина сообщения не станет равной 448 по модулю 512. В итоге, к сообщению добавляется как минимум 1 бит, и как максимум 512.

Шаг 2. Добавление длины сообщения.

64-битное представление ${\displaystyle b}$ (длины сообщения перед добавлением набивочных битов) добавляется к результату предыдущего шага. В маловероятном случае, когда ${\displaystyle b}$ больше, чем ${\displaystyle 2^{64}}$ , используются только 64 младших бита. Эти биты добавляются в виде двух 32-битных слов, и первым добавляется слово, содержащее младшие разряды.

На этом этапе (после добавления битов и длины сообщения) мы получаем сообщение длиной, кратной 512 битам. Это эквивалентно тому, что это сообщение имеет длину, кратную 16-ти 32-битным словам. Пусть ${\displaystyle M[0\ldots N-1]}$ означает массив слов получившегося сообщения (здесь ${\displaystyle N}$ кратно 16).

Шаг 3. Инициализация MD-буфера.

Для вычисления хеша сообщения используется буфер, состоящий из 4 слов (32-битных регистров): ${\displaystyle (A,B,C,D)}$ . Эти регистры инициализируются следующими шестнадцатеричными числами (младшие байты сначала):

       word ${\displaystyle A}$: 01 23 45 67
       word ${\displaystyle B}$: 89 ab cd ef
       word ${\displaystyle C}$: fe dc ba 98
       word ${\displaystyle D}$: 76 54 32 10

Шаг 4. Обработка сообщения блоками по 16 слов.

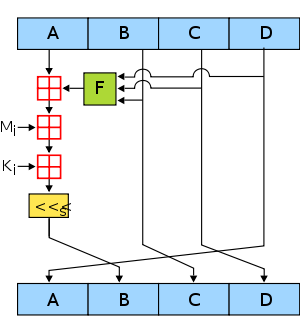
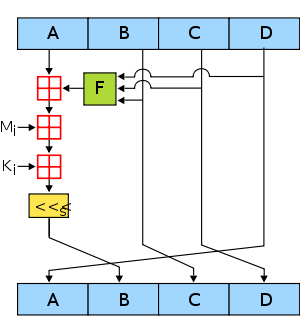
Для начала определим три вспомогательные функции, каждая из которых получает на вход три 32-битных слова, и по ним вычисляет одно 32-битное слово.

      ${\displaystyle F(X,Y,Z)=XY\lor \neg XZ}$
      ${\displaystyle G(X,Y,Z)=XY\lor XZ\lor YZ}$
     ${\displaystyle H(X,Y,Z)=X\oplus Y\oplus Z}$

На каждую битовую позицию ${\displaystyle F}$ действует как условное выражение: если ${\displaystyle X}$ , то ${\displaystyle Y}$ ; иначе ${\displaystyle Z}$ . Функция ${\displaystyle F}$ могла бы быть определена с использованием ${\displaystyle +}$ вместо ${\displaystyle \lor }$ , поскольку ${\displaystyle XY}$ и ${\displaystyle \neg XZ}$ не могут равняться ${\displaystyle 1}$ одновременно. ${\displaystyle G}$ действует на каждую битовую позицию как функция максимального значения: если по крайней мере в двух словах из ${\displaystyle X,Y,Z}$ соответствующие биты равны ${\displaystyle 1}$ , то ${\displaystyle G}$ выдаст ${\displaystyle 1}$ в этом бите, а иначе ${\displaystyle G}$ выдаст бит, равный ${\displaystyle 0}$ . Интересно отметить, что если биты ${\displaystyle X}$ , ${\displaystyle Y}$ и ${\displaystyle Z}$ статистически независимы, то биты ${\displaystyle F(X,Y,Z)}$ и ${\displaystyle G(X,Y,Z)}$ будут также статистически независимы. Функция ${\displaystyle H}$ реализует побитовый ${\displaystyle xor}$ , она обладает таким же свойством, как ${\displaystyle F}$ и ${\displaystyle G}$ .

Алгоритм хеширования на абстрактном языке программирования :

      /* Обрабатываем каждый блок из 16-ти слов */
      for i = 0 to N/16-1 do

        /* Заносим i-ый блок в переменную X */
        for j = 0 to 15 do
          set X[j] to M[i*16+j].
        end /* конец цикла по j */

        /* Сохраняем A как AA, B как BB, C как CC, и D как DD */
        AA = A
        BB = B
        CC = C
        DD = D

        /* Раунд 1 */
        /* Пусть [abcd k s] означает следующую операцию:
             a = (a + F(b,c,d) + X[k]) <<< s. */
        /* Производим 16 следующих операций: */
        [ABCD  0  3]  [DABC  1  7]  [CDAB  2 11]  [BCDA  3 19]
        [ABCD  4  3]  [DABC  5  7]  [CDAB  6 11]  [BCDA  7 19]
        [ABCD  8  3]  [DABC  9  7]  [CDAB 10 11]  [BCDA 11 19]
        [ABCD 12  3]  [DABC 13  7]  [CDAB 14 11]  [BCDA 15 19]

        /* Раунд 2 */
        /* Пусть [abcd k s] означает следующую операцию:
             a = (a + G(b,c,d) + X[k] + 5A827999) <<< s. */
        /* Производим 16 следующих операций: */
        [ABCD  0  3]  [DABC  4  5]  [CDAB  8  9]  [BCDA 12 13]
        [ABCD  1  3]  [DABC  5  5]  [CDAB  9  9]  [BCDA 13 13]
        [ABCD  2  3]  [DABC  6  5]  [CDAB 10  9]  [BCDA 14 13]
        [ABCD  3  3]  [DABC  7  5]  [CDAB 11  9]  [BCDA 15 13]

        /* Раунд 3 */
        /* Пусть [abcd k s] означает следующую операцию:
             a = (a + H(b,c,d) + X[k] + 6ED9EBA1) <<< s. */
        /* Производим 16 следующих операций: */
        [ABCD  0  3]  [DABC  8  9]  [CDAB  4 11]  [BCDA 12 15]
        [ABCD  2  3]  [DABC 10  9]  [CDAB  6 11]  [BCDA 14 15]
        [ABCD  1  3]  [DABC  9  9]  [CDAB  5 11]  [BCDA 13 15]
        [ABCD  3  3]  [DABC 11  9]  [CDAB  7 11]  [BCDA 15 15]

        /* Затем производим следующие операции сложения. (Увеличиваем значение в каждом регистре
           на величину, которую он имел перед началом итерации по i */
        A = A + AA
        B = B + BB
        C = C + CC
        D = D + DD

      end /* конец цикла по i */

Замечание. Величина 5A827999 — шестнадцатеричная 32-битная константа, первые байты — старшие. Она представляет собой квадратный корень из 2 . Она же в восьмеричном представлении: 013240474631. Величина 6ED9EBA1 — шестнадцатеричная 32-битная константа, первые байты — старшие. Она представляет собой квадратный корень из 3. Она же в восьмеричном представлении: 015666365641. Эти данные приведены в книге Кнут, Искусство программирования , издание 1981 года, том 2, стр 660, таблица 2.

Шаг 5. Формирование хеша.

Результат (хеш-функция) получается как ABCD. То есть, мы выписываем 128 бит, начиная с младшего бита A, и заканчивая старшим битом D.

Реализация алгоритма на языке C содержится в .

Примеры хешей

128-битные MD4 хеши представляют собой 32-значное число в 16-ричном формате. В следующем примере показан хеш 43-байтной строки ASCII :

MD4("The quick brown fox jumps over the lazy dog") 
 = 1bee69a46ba811185c194762abaeae90

Любое даже самое незначительное изменение хешируемой информации приводит к получению полностью отличного хеша, например, изменение в примере одной буквы с d на c :

MD4("The quick brown fox jumps over the lazy cog") 
 = b86e130ce7028da59e672d56ad0113df

Пример MD4 хеша для «нулевой» строки:

MD4("") = 31d6cfe0d16ae931b73c59d7e0c089c0

Сравнение с MD5

• MD4 использует три цикла из 16 шагов каждый, в то время как MD5 использует четыре цикла из 16 шагов каждый.

• В MD4 дополнительная константа в первом цикле не применяется. Аналогичная дополнительная константа используется для каждого из шагов во втором цикле. Другая дополнительная константа используется для каждого из шагов в третьем цикле. В MD5 различные дополнительные константы, Т[i], применяются для каждого из 64 шагов.

• MD5 использует четыре элементарные логические функции, по одной на каждом цикле, по сравнению с тремя в MD4, по одной на каждом цикле.

• В MD5 на каждом шаге текущий результат складывается с результатом предыдущего шага. Например, результатом первого шага является измененное слово А. Результат второго шага хранится в D и образуется добавлением А к циклически сдвинутому влево на определенное число бит результату элементарной функции. Аналогично, результат третьего шага хранится в С и образуется добавлением D к циклически сдвинутому влево результату элементарной функции. MD4 это последнее сложение не включает.

Безопасность

Уровень безопасности, закладывавшийся в MD4, был рассчитан на создание достаточно устойчивых гибридных систем электронной цифровой подписи , основанных на MD4 и криптосистеме с открытым ключом. Рональд Ривест считал, что алгоритм хеширования MD4 можно использовать и для систем, нуждающихся в сильной криптостойкости . Но в то же время он отмечал, что MD4 создавался прежде всего как очень быстрый алгоритм хеширования, поэтому он может быть плох в плане криптостойкости. Как показали последовавшие исследования, он был прав, и для приложений, где важна прежде всего криптостойкость, стал использоваться алгоритм MD5 .

Уязвимости

Уязвимости в MD4 были продемонстрированы в статье Берта ден Бура и Антона Босселарса в 1991 году. Первая коллизия была найдена Гансом Доббертином в 1996 году.

См. также

• MD2
• MD5
• HAVAL
• SHA-1

Ссылки

Поиск коллизий