Adler
- 1 year ago
- 0
- 0

Adler-32 — хеш-функция , разработанная Марком Адлером . Является модификацией контрольной суммы Флетчера . Вычисляет значение контрольной суммы в соответствии с для массива байт или его фрагмента. Данный алгоритм расчёта контрольной суммы отличается от CRC32 производительностью. Adler-32 используется в библиотеке Zlib . Rolling checksum версия функции используется в утилите rsync .
Так же, как и в случае контрольной суммы Fletcher, при разработке суммы Adler стояла задача получения контрольной суммы с эффективностью обнаружения ошибок, сравнимой с CRC . Хотя показатели поиска ошибок контрольных сумм Adler и Fletcher практически такие же, как и у относительно слабых CRC, но в некоторых важных случаях они ведут себя гораздо хуже, чем хорошие CRC.
Контрольная сумма Adler-32 получается путём вычисления двух 16-битных контрольных сумм A и Б и конкатенации их бит в 32-битное целое. А равняется сумме всех байт в строке плюс один, а Б является суммой всех отдельных значений А на каждом шаге. В начале выполнения функции Adler-32 А инициализируется единицей, а Б — нулём. Суммы берутся по модулю 65521 (самое большое простое число, меньшее, чем 2 16 ). Байты записываются в сетевом порядке , Б занимает 2 старших байта.
Функция может быть выражена как:
A = 1 + D1 + D2 + ... + Dn (mod 65521) B = (1 + D1) + (1 + D1 + D2) + ... + (1 + D1 + D2 + ... + Dn) (mod 65521) = n×D1 + (n-1)×D2 + (n-2)×D3 + ... + Dn + n (mod 65521) Adler-32(D) = B × 65536 + A
где D — строка байт, для которых должна быть вычислена контрольная сумма, а n — длина D.
Значение Adler-32 для ASCII строки «Wikipedia» вычисляется следующим образом:
ASCII code A B (в десятиричном виде) W: 87 1 + 87 = 88 0 + 88 = 88 i: 105 88 + 105 = 193 88 + 193 = 281 k: 107 193 + 107 = 300 281 + 300 = 581 i: 105 300 + 105 = 405 581 + 405 = 986 p: 112 405 + 112 = 517 986 + 517 = 1503 e: 101 517 + 101 = 618 1503 + 618 = 2121 d: 100 618 + 100 = 718 2121 + 718 = 2839 i: 105 718 + 105 = 823 2839 + 823 = 3662 a: 97 823 + 97 = 920 3662 + 920 = 4582 A = 920 = 398 hex (base 16) B = 4582 = 11E6 hex Output = 300286872 = 11E60398 hex
Операция сложения по модулю не даёт никакого эффекта в этом примере, так как ни одно из значений не достигло 65521.
Алгоритм вычисления контрольной суммы Adler идентичен алгоритму вычисления суммы Fletcher за исключением некоторых отличий. Первое отличие состоит в том, что в случае функции Adler сумма А инициализируется значением 1. Второе отличие между двумя алгоритмами в том, что сумма в алгоритме Adler-32 вычисляется по модулю простого числа 65521, когда как суммы Fletcher вычисляются по модулю -1, -1, -1 (в зависимости от используемого количества бит), которые являются составными числами . Это изменение в алгоритме было сделано с целью достижения лучшего перемешивания бит. Использование простого числа позволяет функции Adler-32 замечать различия в некоторых комбинациях байт, которые функция Fletcher не способна зафиксировать. Третье отличие, которое наиболее сильно влияет на скорость алгоритма, заключается в том, что суммы функции Adler-32 вычисляются над 8-битными, а не над 16-битными словами, что приводит к удвоению числа итераций цикла. Это приводит к тому, что вычисление контрольной суммы Adler-32 занимает от полутора до двух раз большее количество времени, чем контрольная сумма Fletcher для данных, разбитых на 16-битные слова. Для данных, разбитых на байты, Adler-32 работает быстрее, чем алгоритм Fletcher.
Хотя контрольная сумма Adler не определена официально для других длин слов данных, можно использовать самое большое простое целое меньшее 2 4 =16 и 2 8 =256, чтобы реализовать 8- и 16-битные контрольные суммы Adler для целей сравнения. Имея похожий алгоритм, контрольная сумма Adler имеет схожую производительность с суммой Fletcher. Все 2-битные ошибки обнаружены для слов данных длиной меньше, чем M*(k/2) бит, где k — размер контрольной суммы, M равняется модулю суммы Adler. Как и в случае с контрольной суммой Fletcher, наихудшее значение вероятности необнаруженной ошибки наблюдается при одинаковом количестве нулей и единиц в каждом блоке данных. Adler-8 и Adler-16 обнаруживают все групповые ошибки длиной меньше, чем k/2 бит. Adler-32 обнаруживает все групповые ошибки длиной не более 7 бит. Рисунок1 показывает зависимость вероятности необнаруженных ошибок для контрольных сумм Adler и Fletcher для частоты битовых ошибок 10 −5 .
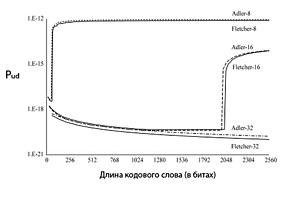
Лучшее перемешивание бит, которое обеспечивает контрольная сумма Adler, должно было привести к лучшим показателям поиска ошибок, чем у суммы Fletcher. Но, как показывает , Fletcher-32 работает лучше, чем Adler-32 на 8 KB. Контрольная сумма Adler превосходит сумму Fletcher только в случае 16-битных контрольных сумм, и при этом только в той области этих сумм, где расстояние Хэмминга равно 3. Проблема в том, что, несмотря на то, что простое число, использованное в качестве модуля операции, приводит к лучшему перемешиванию бит, в результате получается меньшее количество правильных значений проверочных контрольных сумм, доступных для кодовых слов. В большинстве случаев это сводит на нет положительный эффект лучшего перемешивания. Таким образом, контрольная сумма Fletcher превосходит сумму Adler во всех случаях, кроме суммы Adler-16, применяемой к коротким словам данных. Даже увеличение эффективности поиска ошибок, возможно, не стоит увеличения вычислительных накладных расходов, к которым приводит использование модульных операций.
Авторы
провели сравнение эффективности обнаружения ошибок. Свод полученных ими результатов представлен в таблице:
| Алгоритм | d | Block | i/byte | T size | T-look | P udb | P uds |
|---|---|---|---|---|---|---|---|
| Adler-32 | 3 | 2 19 | 3 | - | - | 10 −36 | 10 −35 |
| Fletcher-32 | 3 | 2 19 | 2 | - | - | 10 −37 | 10 −36 |
| IEEE-802 | 3 | 2 16 | 2.75 | 2 18 | 0.5/b | 10 −41 | 10 −40 |
| CRC32C | 3 | 2 31 −1 | 2.75 | 2 18 | 0.5/b | 10 −41 | 10 −40 |
В таблице: d — минимальное расстояние на блоке длины Block, Block — длина блока в битах, i/byte — количество программных инструкций, приходящихся на байт, T
size
— размер таблицы (в случае, если необходим просмотр), T-look — число просмотров на байт, P
udb
— вероятность необнаруженных групповых ошибок, P
uds
— вероятность необнаруженных единичных ошибок.
Вероятности необнаруженных ошибок в таблице, приведённой выше, вычислены в предположении равномерной распределённости данных.
«Хорошая» хеш-функция отличается более-менее равномерным распределением вычисленных значений. Очевидно, что Adler-32 не удовлетворяет этому требованию для коротких данных (максимальное значение A для 128-байтного сообщения равняется 32640, которое меньше, чем 65521 — число, по которому берется операция модуля). Из-за этого недостатка разработчики протокола SCTP предпочли этому алгоритму CRC32 , так как в сетевом протоколе необходимо хеширование коротких последовательностей байт.
Точно как и для CRC32 , для Adler-32 можно легко сконструировать коллизию , то есть для данного хеша найти другие исходные данные, имеющие то же значение функции.
Имеет преимущество над CRC32 в том, что она быстрее вычисляется программными средствами.
Простой реализацией алгоритма на языке Си является следующий код:
uint32_t adler32( const unsigned char* buf, size_t buf_length )
{
uint32_t s1 = 1;
uint32_t s2 = 0;
while( buf_length-- )
{
s1 = ( s1 + *( buf++ ) ) % 65521;
s2 = ( s2 + s1 ) % 65521;
}
return ( s2 << 16 ) + s1;
}
Эффективную реализацию смотрите в коде библиотеки zlib .