Хеш-функции Дженкинса представляют собой семейство хеш-функций общего назначения для ключей переменной длины, разработанных Бобом Дженкинсом. Функции также могут использоваться в качестве контрольной суммы для обнаружения случайного повреждения данных или обнаружения идентичных записей в базе данных . Впервые описание функции было опубликовано в 1997 году.

Хеш-функции

one-at-a-time

Приведенный текст функции взят с веб-страницы Боба Дженкинса и является расширенной версией, опубликованной автором в журнале доктора Доббса.

uint32_t jenkins_one_at_a_time_hash( unsigned char *key, size_t len)
{
    uint32_t hash, i;
    for(hash = i = 0; i < len; ++i)
    {
        hash += key[i];
        hash += (hash << 10);
        hash ^= (hash >> 6);
    }
    hash += (hash << 3);
    hash ^= (hash >> 11);
    hash += (hash << 15);
    return hash;
}

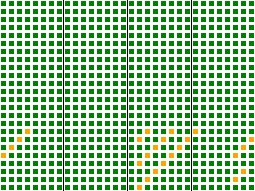
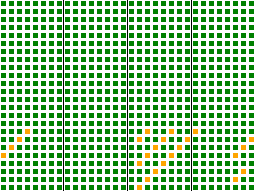
На рисунке справа показан лавинный эффект функции.

Каждая из 24 строк соответствует одному биту в 3-байтовом ключе на входе и каждый из 32 столбцов соответствует биту в выходном хеше. Цвета показывают, насколько хорошо входной бит влияет на данный бит на выходе: зеленый квадрат указывает хорошее перемешивание, желтый квадрат — слабое перемешивание, и красный обозначал бы, что перемешивания не происходит. Как видно из рисунка, только несколько битов в последнем байте входного ключа слабо перемешаны с несколькими битами результата.

lookup2

Функция lookup2 была промежуточным вариантом функции one-at-a-time.

lookup3

Функция lookup3 разбивает вход на блоки по 12 байт в каждом (96 бит). Такое поведение может быть более целесообразным, когда скорость важнее, чем простота. Имейте в виду, что увеличение скорости работы при использовании этого варианта хеша вероятно только для больших ключей, и что повышенная сложность реализации, наоборот, может вызвать замедление работы. Например, вследствие того, что компилятор может оказаться не в состоянии подставить функцию инлайн.

Ссылки