Interested Article - Hamsi

- 2021-08-16
- 1
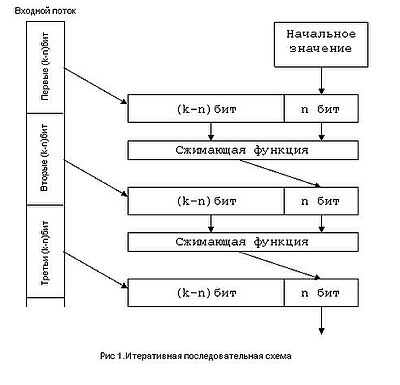
Hamsi — криптографическая хеш-функция , в основу которой положены алгоритмы и Serpent . Эта хеш-функция не запатентована и является общественным достоянием . Существуют две разновидности алгоритма : Hamsi-256 и Hamsi-512. В основе алгоритма лежат функция разложения и циклическая трансформация . Циклическая трансформация работает с четырьмя строками матрицы состояний. Число столбцов этой матрицы равно 4 для Hamsi-256, 8 для Hamsi-512. Элементами матрицы являются слова размером 32 бита .
История
Hamsi была одним из участников в открытом конкурсе SHA-3 Национального института стандартов и технологий по разработке новых криптографических хеш-функций , которые преобразуют сообщения переменной длины в сжатые текстовые строки фиксированной длины, что может быть использовано для электронно-цифровых подписей , аутентификации сообщений и других применений. В первом раунде соревнования приняли участие 51 кандидат. 14 из них (включая Hamsi) прошли во второй тур . Однако Hamsi не попала в число 5 кандидатов последнего тура, объявленных 10 декабря 2010 года .
Описание
Общая структура
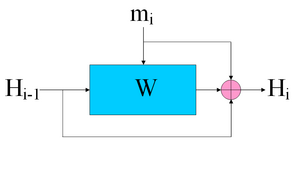
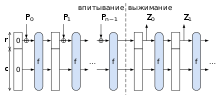
Hamsi использует такие преобразования, как конкатенация ( англ. Concatenation ), перестановка ( англ. Permutation ) и округление ( англ. Truncation ), которые также используются в других алгоритмах хеширования , например Snefru и . В алгоритме также применяется функции расширения текста сообщения ( англ. Message expansion ) и распространения связывающего значения ( англ. Chaining value ) на каждой итерации . Для нелинейных перестановок ( англ. Non-linear Permitations ) используются линейные преобразования и один S-box из блочного шифрования Serpent . Общую структуру Hamsi можно представить в виде:
| 1 | Message Expansion | E : {0, 1} → {0, 1} |
| 2 | Concatenation | C : {0, 1} x {0, 1} → {0, 1} |
| 3 | Non-linear Permutations | P,P : {0, 1} → {0, 1} |
| 4 | Truncation | T : {0, 1} → {0, 1} |
Обозначения:
| F | Конечное поле из n элементов |
| <<< | Циклический сдвиг влево |
| Исключающее ИЛИ ( XOR ) | |
| << | Битовый сдвиг влево |
| [n, m, d] | Код длины n, размерностью m и минимальным расстоянием d |
Значения m, n и s для различных вариантов Hamsi представлены в следующей таблице:
| m | n | s | |
| Hamsi-256 | 32 | 256 | 512 |
| Hamsi-512 | 64 | 512 | 1024 |
Пусть (M 1 ||M 2 ||M 3 || . . . ||M ||) уже дополненное сообщение, тогда разновидности Hamsi могут быть описаны следующим образом:
Hamsi-256:
h = (T ◦ P ◦ C(E(M ), h −1)) ⊕ h −1, h = v 256 , 0 < <
h = (T ◦ P ◦ C(E(M ), h −1)) ⊕ h −1
Hamsi-512:
h = (T ◦ P ◦ C(E(M ), h −1)) ⊕ h −1, h = v 512 , 0 < <
h = (T ◦ P ◦ C(E(M ), h −1)) ⊕ h −1
Начальные значения
Начальным значением для алгоритма является начальное значение связывающего значения h . Оно получено с помощью кодировки UTF-8 следующего сообщения: «Ozgul Kucuk, Katholieke Universiteit Leuven, Departement Elektrotechniek, Computer Security and Industrial Cryptography, Kasteelpark Arenberg 10, bus 2446, B-3001 Leuven-Heverlee, Belgium.» Начальные значения для различных разновидностей алгоритма представлены в следующей таблице:
| v 256 |
|
||||
| v 512 |
|
Дополнение сообщения
Hamsi оперирует с блоками сообщений длиной 32 и 64 бита для алгоритмов Hamsi-256 и Hamsi-512 соответственно. Если длина блока меньше чем необходимо, тогда происходит дополнение сообщения ( англ. Message padding ). Дополнение происходит следующим образом. К сообщению справа добавляется один бит значением '1', а затем добавляются биты со значениями равными '0' до тех пор пока длина сообщения не станет равной 32 или 64. Пример:
Есть сообщение длиной 24 бита
| 1010 0110 1110 1111 1111 0000 |
После дополнения до 32-х битного оно будет выглядеть так
| 1010 0110 1110 1111 1111 0000 | 1000 0000 |
Расширение сообщения
Hamsi использует линейные коды для расширения сообщений. Для Hamsi-256 расширение сообщения длиной 32 бита в сообщение длиной 256 бит производится с помощью кода [128, 16, 70] над полем F . Для Hamsi-512 расширение сообщения длиной 64 бита в сообщение длиной 512 бит производится с помощью кода [256, 32, 131] над полем F .
Конкатенация
К словам расширенного сообщения (m ,m , . . . ,m ) приписывается связывающее значение (c , c , . . . , c ). Значения i и j равны 7 для Hamsi-256 и 15 для Hamsi-512. Затем над полученным сообщением будет произведена нелинейная перестановка P. Метод конкатенации определяет порядок следования битов на входе Р.
В Hamsi-256
C: {0, 1} x{0, 1} → {0, 1} , а подробнее
C(m ,m 1 , . . . ,m 7 , c 0 , c 1 , . . . , c 7 ) = (m 0 ,m 1 , c 0 , c 1 , c 2 , c 3 ,m 2 ,m 3 ,m 4 , m 5 , c 4 , c 5 , c 6 , c 7 ,m 6 ,m 7 )
Порядок слов легче всего запомнить с помощью следующей таблицы, результат из которой можно получить построчным считыванием:
| m 0 | m 1 | c 0 | c 1 |
| c 2 | c 3 | m 2 | m 3 |
| m 4 | m 5 | c 4 | c 5 |
| c 6 | c 7 | m 6 | m 7 |
В Hamsi-512
C: {0, 1} × {0, 1} → {0, 1} , а подробнее
C(m 0 ,m 1 , . . . ,m 14 ,m 15 , c 0 , c 1 , . . . , c 14 , c 15 ) = (m 0 ,m 1 , c 0 , c 1 ,m 2 ,m 3 , c 2 , c 3 , c 4 , c 5 ,m 4 ,m 5 , c 6 , c 7 ,m 6 ,m 7 ,m 8 , m 9 , c 8 , c 9 ,m 10 ,m 11 , c 10 , c 11 , c 12 , c 13 ,m 12 ,m 13 , c 14 , c 15 ,m 14 ,m 15 )
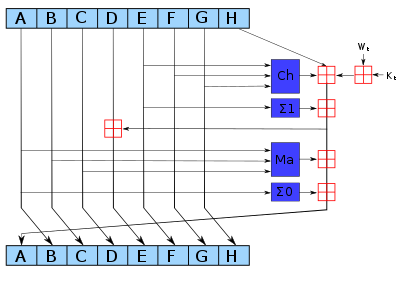
Нелинейная перестановка P
Нелинейная перестановка состоит из трех этапов
- Над входными битами , константами и счетчиком выполняется операция XOR
- Затем следует применение 4-битных S-боксов
- И наконец несколько применений линейного преобразования L
Все это повторяется столько раз, сколько задано количество циклов. На вход каждый раз поступает сообщение (s 0 , s 1 , s 2 , . . . , s j ), где j равно 15 для Hamsi-256 и 31 для Hamsi-512.
1) Прибавление констант и счетчика
На этом этапе над входным сообщением, константами и счетчиком выполняется операция XOR . Счетчик определяет номер выполненного цикла. Для первого цикла c равен 0, для второго с = 1 и так далее. Используемые константы приведены в следующей таблице:
| α 0 = 0xff00f0f0 | α 1 = 0xccccaaaa | α 2 = 0xf0f0cccc | α 3 = 0xff00aaaa |
| α 4 = 0xccccaaaa | α 5 = 0xf0f0ff00 | α 6 = 0xaaaacccc | α 7 = 0xf0f0ff00 |
| α 8 = 0xf0f0cccc | α 9 = 0xaaaaff00 | α 10 = 0xccccff00 | α 11 = 0xaaaaf0f0 |
| α 12 = 0xaaaaf0f0 | α 13 = 0xff00cccc | α 14 = 0xccccf0f0 | α 15 = 0xff00aaaa |
| α 16 = 0xccccaaaa | α 17 = 0xff00f0f0 | α 18 = 0xff00aaaa | α 19 = 0xf0f0cccc |
| α 20 = 0xf0f0ff00 | α 21 = 0xccccaaaa | α 22 = 0xf0f0ff00 | α 23 = 0xaaaacccc |
| α 24 = 0xaaaaff00 | α 25 = 0xf0f0cccc | α 26 = 0xaaaaf0f0 | α 27 = 0xccccff00 |
| α 28 = 0xff00cccc | α 29 = 0xaaaaf0f0 | α 30 = 0xff00aaaa | α 31 = 0xccccf0f0 |
В Hamsi-256
(s 0 , s 1 , . . . , s 15 ) := (s 0 ⊕ α 0 , s 1 ⊕ α 1 ⊕ c, s 2 , . . . , s 15 ⊕ α 15 )
В Hamsi-512
(s 0 , s 1 , . . . , s 31 ) := (s 0 ⊕ α 0 , s 1 ⊕ α 1 ⊕ c, s 2 , . . . , s 31 ⊕ α 31 )
2) Этап подстановки
На этом этапе происходит подстановка 4-битных S-боксов , взятых из алгоритма Serpent . Hamsi очень удобно спроектирован для параллельного вычисления . Все 128 идентичных S-боксов (256 для Hamsi-512) могут обсчитываться в одно и то же время, что ускоряет работу алгоритма. S-box используемый в Hamsi:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| s[x] | 8 | 6 | 7 | 9 | 3 | C | A | F | D | 1 | E | 4 | 0 | B | 5 | 2 |
3) Этап преобразования
Этап преобразования основан на нескольких применениях линейного преобразования L: {0, 1} → {0, 1} . L оперирует с 32-битными словами. В общем виде преобразование можно записать в виде (s i , s j , s k , s l ) := L(s i , s j , s k , s l ) .
Более подробное описание преобразования L(a, b, c, d) :
a := a <<< 13
c := c <<< 3
b := b ⊕ a ⊕ c
d := d ⊕ c ⊕ (a << 3)
b := b <<< 1
d := d <<< 7
a := a ⊕ b ⊕ d
c := c ⊕ d ⊕ (b << 7)
a := a <<< 5
c := c <<< 22
Округление
Округление T : {0, 1} 512 → {0, 1} 256 в Hamsi-256 определяется следующим образом:
T (s 0 , s 1 , s 2 , . . . , s 14 , s 15 ) = (s 0 , s 1 , s 2 , s 3 , s 8 , s 9 , s 10 , s 11 )
В Hamsi-512 округление T : {0, 1} 1024 → {0, 1} 512 определяется так:
T (s 0 , s 1 , s 2 , . . . , s 30 , s 31 ) = (s 0 , s 1 , s 2 , s 3 , s 4 , s 5 , s 6 , s 7 , s 16 , s 17 , s 18 , s 19 , s 20 , s 21 , s 22 , s 23 )
Округление осуществляется после финального цикла нелинейной перестановки.
Нелинейная перестановка P f
Нелинейные перестановки P и P f отличаются только константами. Также P f применяется только к последнему блоку сообщений как финальное преобразование.
Константы для P f :
| α 0 = 0xcaf9639c | α 1 = 0x0ff0f9c0 | α 2 = 0x639c0ff0 | α 3 = 0xcaf9f9c0 |
| α 4 = 0x0ff0f9c0 | α 5 = 0x639ccaf9 | α 6 = 0xf9c00ff0 | α 7 = 0x639ccaf9 |
| α 8 = 0x639c0ff0 | α 9 = 0xf9c0caf9 | α 10 = 0x0ff0caf9 | α 11 = 0xf9c0639c |
| α 12 = 0xf9c0639c | α 13 = 0xcaf90ff0 | α 14 = 0x0ff0639c | α 15 = 0xcaf9f9c0 |
| α 16 = 0x0ff0f9c0 | α 17 = 0xcaf9639c | α 18 = 0xcaf9f9c0 | α 19 = 0x639c0ff0 |
| α 20 = 0x639ccaf9 | α 21 = 0x0ff0f9c0 | α 22 = 0x639ccaf9 | α 23 = 0xf9c00ff0 |
| α 24 = 0xf9c0caf9 | α 25 = 0x639c0ff0 | α 26 = 0xf9c0639c | α 27 = 0x0ff0caf9 |
| α 28 = 0xcaf90ff0 | α 29 = 0xf9c0639c | α 30 = 0xcaf9f9c0 | α 31 = 0x0ff0639c |
Количество циклов
Количество циклов для различных вариантов Hamsi приведены в таблице:
| Hamsi-256 | Hamsi-512 | |
| P циклов | 3 | 6 |
| P f циклов | 6 | 12 |
Во втором туре соревнования SHA-3 появилась новая модификация алгоритма под названием Hamsi-256/8. Её отличие от Hamsi-256 в том, что количество P f циклов теперь равно 8.
Примечания
- L. R. Knudsen, C. Rechberger, S. S. Thomsen. (неопр.) // Lecture Notes in Computer Science. — 2007. — Т. 4593 . — С. 39—57 . — doi : . 15 сентября 2012 года.
- от 13 января 2013 на Wayback Machine .
- . Дата обращения: 28 ноября 2009. 9 июля 2011 года.
- . Дата обращения: 28 ноября 2009. 17 июня 2015 года.
- . Дата обращения: 28 ноября 2009. 10 апреля 2012 года.
- . Дата обращения: 15 июня 2015. 14 марта 2011 года.
- Merkle R.C. A Fast Software One-Way Hash Function. Journal of Cryptology, 3(1):43-58, 1990
- J.H. van Lint. Introduction to Coding Theory
- Bounds on the minimum distance of linear codes. (недоступная ссылка)
Литература
- Özgül Kücük. (PDF) (31 октября 2008). Дата обращения: 11 декабря 2008. 11 апреля 2012 года.
- 2021-08-16
- 1