Lúffa (хеш-функция, произносится как «люффа») — криптографический алгоритм (семейство алгоритмов) хеширования переменной разрядности, разработанный Даи Ватанабэ ( англ. Dai Watanabe ), Хисайоши Сато ( англ. Hisayoshi Sato ) из Hitachi и Кристофом Де Канньере ( нидерл. Christophe De Cannière ) из исследовательской группы COSIC ( ) Лёвенского католического университета для участия в конкурсе , Национального института стандартов и технологий США ( NIST ). Lúffa является вариантом функции губки , предложенной Гвидо Бертони ( англ. Guido Bertoni ) и соавторами, криптостойкость которой основана только на случайности основной перестановки. В отличие от оригинальной функции губки , Lúffa использует множественное число параллельных перестановок и функции инжекции сообщений.

История участия в конкурсе NIST SHA-3

• 9 декабря 2008 года Luffa в числе 51 кандидата прошла в первый раунд конкурса SHA-3 .
• 25-28 февраля 2009 года хеш-функция была представлена на конференция NIST .
• 24 июля 2009 года был опубликован список из 14 кандидатов прошедших во второй раунд, в который вошла Luffa.
• 23-24 августа 2010 года состоялась конференция , на которой были рассмотрены кандидаты , прошедшие во второй раунд.
• 10 декабря 2010 года произошло объявление 5 кандидатов последнего тура конкурса SHA-3 , Luffa выбыла из соревнования из-за низкой криптостойкости функции сжатия .

Алгоритм Lúffa

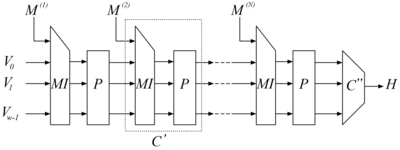
Обработка сообщения производится цепочкой раундовых функций смешивания с фиксированной входной и выходной длиной, которая представляет собой функцию губку . Цепочка состоит из блоков промежуточного смешивания C’ (раундовых функций) и блока завершения C’’. Раундовые функции образованы семейством нелинейных перестановок, так называемых шаговых функций. На вход функции первого раунда ${\displaystyle (i=1)}$ подается ${\displaystyle (M^{(1)},V_{0},\ V_{1},\cdots ,\ V_{w-1})}$ : первый блок сообщения ${\displaystyle M^{(1)}}$ и инициализирующие значения ${\displaystyle V_{0},\ V_{1},\cdots ,\ V_{w-1}}$ , где ${\displaystyle w}$ — количество перестановок. Входными параметрами ${\displaystyle i}$ -го раунда является ${\displaystyle (M^{(i)},H_{0}^{(i-1)},\ H_{1}^{(i-1)},\cdots ,\ H_{w-1}^{(i-1)})}$ : выход предыдущего ${\displaystyle (i-1)}$ раунда и ${\displaystyle i}$ -й блок сообщения ${\displaystyle M^{(i)}}$ .

Дополнение сообщения

Дополнение сообщения ${\displaystyle M}$ длины ${\displaystyle l}$ до кратности 256 битам производится строкой ${\displaystyle 1000\cdots 0}$ , где число нулей ${\displaystyle k}$ определяется из сравнения ${\displaystyle l+1+k\equiv 0\mod 256}$

Инициализация

Кроме первого блока сообщения ${\displaystyle M^{(1)}}$ на вход функции первого раунда в качестве инициализурующих значений подаются векторы ${\displaystyle V_{i}}$ .

${\displaystyle V_{i,j}}$
i	j
	0	1	2	3	4	5	6	7
0	0x 6d251e69	0x 44b051e0	0x 4eaa6fb4	0x dbf78465	0x 6e292011	0x 90152df4	0x ee058139	0x def610bb
1	0x c3b44b95	0x d9d2f256	0x 70eee9a0	0x de099fa3	0x 5d9b0557	0x 8fc944b3	0x cf1ccf0e	0x 746cd581
2	0x f7efc89d	0x 5dba5781	0x 04016ce5	0x ad659c05	0x 0306194f	0x 666d1836	0x 24aa230a	0x 8b264ae7
3	0x 858075d5	0x 36d79cce	0x e571f7d7	0x 204b1f67	0x 35870c6a	0x 57e9e923	0x 14bcb808	0x 7cde72ce
4	0x 6c68e9be	0x 5ec41e22	0x c825b7c7	0x affb4363	0x f5df3999	0x 0fc688f1	0x b07224cc	0x 03e86cea

Раундовая функция

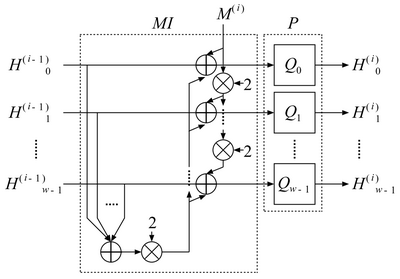
Раундовая функция является последовательным применением функции инжекции сообщения MI и перестановочной функции P.

Функции инжекции сообщения

Функция инжекции сообщения может быть представлена в виде матрицы преобразования над кольцом ${\displaystyle GF(2^{8})^{32}}$ . Порождающий полином поля ${\displaystyle f(x)=x^{8}+x^{4}+x^{3}+x+1}$ .

Функции инжекции сообщения ${\displaystyle w=3}$

${\displaystyle {\begin{pmatrix}X_{0}\\X_{1}\\X_{2}\end{pmatrix}}={\begin{pmatrix}3&2&2&1\\2&3&2&2\\2&2&3&4\end{pmatrix}}{\begin{pmatrix}H_{0}^{(i-1)}\\H_{1}^{(i-1)}\\H_{2}^{(i-1)}\\M_{i}\end{pmatrix}}}$

где числа ${\displaystyle {1,2,3,4}}$ соответственно обозначают полиномы ${\displaystyle {1,x,x+1,x^{2}}}$

Функции инжекции сообщения ${\displaystyle w=4}$

${\displaystyle {\begin{pmatrix}X_{0}\\X_{1}\\X_{2}\\X_{3}\end{pmatrix}}={\begin{pmatrix}4&6&6&7&1\\7&4&6&6&2\\6&7&4&6&4\\6&6&7&4&8\end{pmatrix}}{\begin{pmatrix}H_{0}^{(i-1)}\\H_{1}^{(i-1)}\\H_{2}^{(i-1)}\\H_{3}^{(i-1)}\\M_{i}\end{pmatrix}}}$

Функции инжекции сообщения ${\displaystyle w=5}$

${\displaystyle {\begin{pmatrix}X_{0}\\X_{1}\\X_{2}\\X_{3}\\X_{4}\end{pmatrix}}={\begin{pmatrix}0F&08&0A&0A&08&01\\08&0F&08&0A&0A&02\\0A&08&0F&08&0A&04\\0A&0A&08&0F&08&08\\08&0A&0A&08&0F&10\end{pmatrix}}{\begin{pmatrix}H_{0}^{(i-1)}\\H_{1}^{(i-1)}\\H_{2}^{(i-1)}\\H_{3}^{(i-1)}\\H_{4}^{(i-1)}\\M_{i}\end{pmatrix}}}$

Функция перестановки

Нелинейная функция перестановки имеет ${\displaystyle w\cdot n_{b}}$ битовый вход, длина суб-перестановки — ${\displaystyle n_{b}}$ фиксирована в спецификации Lúffa , ${\displaystyle n_{b}=256}$ ; количество — ${\displaystyle w}$ перестановок зависит от размера хеша и приведено в таблице.

Длина хеша ${\displaystyle n_{h}}$	Количество перестановок ${\displaystyle w}$
224	3
256	3
384	4
512	5

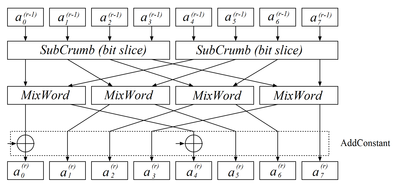
Функция перестановки является восьмикратным повторением шаговой функции над блоком ${\displaystyle Q_{i}}$ , полученным из функции инжекции сообщения ${\displaystyle MI}$ . Блок ${\displaystyle Q_{i}}$ представляется в виде 8 32-битных слов: ${\displaystyle a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7}}$ . Шаговая функция состоит из 3 функций: SubCrumb, MixWord, AddConstant.

Permute(a[8], j){ //Permutation Q_j
  for (r = 0; r < 8; r++){
    SubCrumb(a[0],a[1],a[2],a[3]);
    SubCrumb(a[5],a[6],a[7],a[4]);
    for (k = 0; k < 4; k++)
      MixWord(a[k],a[k+4]);
    AddConstant(a, j, r);
  }
}

SubCrumb

SubCrumb — функция замены l-х битов в ${\displaystyle a_{0},a_{1},a_{2},a_{3}}$ или ${\displaystyle a_{4},a_{5},a_{6},a_{7}}$ по S-блоку ${\displaystyle S[16]={13,14,0,1,5,10,7,6,11,3,9,12,15,8,2,4}}$ , результатом выполнения является замена ${\displaystyle a_{i}\rightarrow x_{i}}$ , индекс ${\displaystyle i}$ S-блока получается в результате конкатенации соответствующих битов ${\displaystyle a_{j,l}}$ : ${\displaystyle i=a_{3,l}||a_{2,l}||a_{1,l}||a_{0,l}}$ , биты ${\displaystyle x_{j,l}}$ заменяются на соответствующие биты из ${\displaystyle S[i]}$ по следующей схеме:

1. ${\displaystyle x_{3,l}||x_{2,l}||x_{1,l}||x_{0,l}=S[i]=S[a_{3,l}||a_{2,l}||a_{1,l}||a_{0,l}],0\leq l<32}$
2. ${\displaystyle x_{4,l}||x_{7,l}||x_{6,l}||x_{5,l}=S[i]=S[a_{4,l}||a_{7,l}||a_{6,l}||a_{5,l}],0\leq l<32,}$

MixWord

MixWord — линейная функция перестановки, на вход принимает ${\displaystyle x_{k}}$ и ${\displaystyle x_{k+4}}$ , ${\displaystyle 0\leq k<4}$ ; выходом являются ${\displaystyle y_{k}}$ и ${\displaystyle y_{k+4}}$ , полученные по алгоритму:

1. ${\displaystyle y_{k+4}=x_{k+4}\oplus x_{k}}$
2. ${\displaystyle y_{k}=x_{k}<<<2}$ , (<<< 2 — циклический сдвиг влево на 2 бита)
3. ${\displaystyle y_{k}=y_{k}\oplus y_{k+4}}$
4. ${\displaystyle y_{k+4}=y_{k+4}<<<14}$
5. ${\displaystyle y_{k+4}=y_{k+4}\oplus y_{k}}$
6. ${\displaystyle y_{k}=y_{k}<<<10}$
7. ${\displaystyle y_{k}=y_{k}\oplus y_{k+4}}$
8. ${\displaystyle y_{k+4}=y_{k+4}<<<1}$

AddConstant

AddConstant — функция добавления константы ${\displaystyle c_{j,k}^{(r-1)}}$ к ${\displaystyle a_{j,k}^{(r-1)}}$

${\displaystyle a_{j,k}^{(r)}=a_{j,k}^{(r-1)}\oplus c_{j,k}^{(r-1)},k=0,4}$

Таблица констант приведена в дополнении B к спецификации Lúffa .

Блок завершения

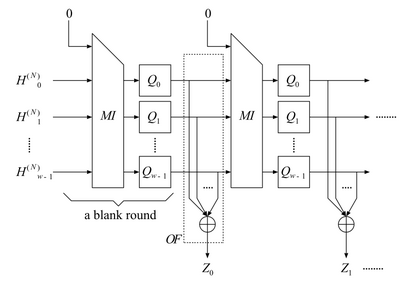
Завершающий этап формирования дайджеста сообщения состоит из последовательных итераций функции выхода и раундовой функции с нулевым блоком сообщения 0x00 ${\displaystyle \cdots }$ 0 на входе. Функция выхода представляет собой XOR всех промежуточных значений, а в качестве результата представляет 256-битное слово ${\displaystyle Z_{i}}$ . На i -й итерации значение выходной функции определяется как

${\displaystyle Z_{i}=\bigoplus _{k=0}^{w-1}H_{k}^{(N+j)}}$ , где ${\displaystyle j=i}$ , если ${\displaystyle N=1}$ , иначе ${\displaystyle j=i+1}$

Через ${\displaystyle Z_{i,j}}$ обозначим 32-битные слова в ${\displaystyle Z_{i}}$ , тогда выходом Lúffa являются составленные последовательно ${\displaystyle Z_{i,j}}$ . Символ "||" обозначает конкатенацию.

Длина хеша ${\displaystyle n_{h}}$	Значение хеша ${\displaystyle H}$
224	${\displaystyle Z_{0,0}||\cdots ||Z_{0,6}}$
256	${\displaystyle Z_{0,0}||\cdots ||Z_{0,7}}$
384	${\displaystyle Z_{0,0}||\cdots ||Z_{0,6}||Z_{1,0}||\cdots ||Z_{1,3}}$
512	${\displaystyle Z_{0,0}||\cdots ||Z_{0,6}||Z_{1,0}||\cdots ||Z_{1,7}}$

Хеш Lúffa-224 фактически представляет собой хеш Lúffa-256 без последнего 32-битного слова.

Тестовые векторы

Дайджесты сообщения «abc» при различном размере хеша .

	224	256	384	512
Z 0,0	0x f29311b8	0x f29311b8	0x 9a7abb79	0x f4024597
Z 0,1	0x 7e9e40de	0x 7e9e40de	0x 7a840e2d	0x 3e80d79d
Z 0,2	0x 7699be23	0x 7699be23	0x 423c34c9	0x 0f4b9b20
Z 0,3	0x fbeb5a47	0x fbeb5a47	0x 1f559f68	0x 2ddd4505
Z 0,4	0x cb16ea4f	0x cb16ea4f	0x 09bdb291	0x b81b8830
Z 0,5	0x 5556d47c	0x 5556d47c	0x 6fb2e9ef	0x 501bea31
Z 0,6	0x a40c12ad	0x a40c12ad	0x fec2fa0a	0x 612b5817
Z 0,7		0x 764a73bd	0x 7a69881b	0x aae38792
Z 1,0			0x e9872480	0x 1dcefd80
Z 1,1			0x c635d20d	0x 8ca2c780
Z 1,2			0x 2fd6e95d	0x 20aff593
Z 1,3			0x 046601a7	0x 45d6f91f
Z 1,4				0x 0ee6b2ee
Z 1,5				0x e113f0cb
Z 1,6				0x cf22b643
Z 1,7				0x 81387e8a

Криптоанализ

В ходе второго тура конкурса SHA-3 Luffa-224 и Luffa-256 в первоначальном варианте показали низкую криптостойкость, для успешной атаки потребовалось ${\displaystyle 2^{216}}$ сообщений. После чего, алгоритм был модифицирован Даи Ватанабэ и получил название Luffa v.2. Изменения Luffa v.2 :

• добавлен пустой раунд функции завершения для всех размеров хеша
• изменен S-блок
• увеличено количество повторений шаговой функции с 7 до 8

Барт Пренель (Bart Preneel) представил успешную атаку по поиску коллизий для 4 раундов шаговой функции Luffa за ${\displaystyle 2^{90}}$ операций хеширования и ${\displaystyle 2^{224}}$ для 5-раундовой, показав тем самым границу стойкости дизайна к диференциальному поиску коллизий.

Производительность

В 2010 году Томас Оливиера и Джулио Лопез провели успешные исследования возможности увеличения производительности оригинальной реализации Luffa. Оптимизированная реализация алгоритма имеет 20 % увеличение производительности вычисления хеша Luffa-512 при исполнении в 1 потоке, для Luffa-256/384 прирост производительности однопоточной реализации в различных тестах составляет не более 5 %. Результаты тестов приведены в таблице в :

• На 64-битных платформах без SSE:

Реализация алгоритма	Luffa-256	Luffa-384	Luffa-512
Оригинальная реализация 2009 год
Однопоточная реализация	27	42	58
Томас Оливиера 2010 год
Однопоточная реализация	24	42	46
Многопоточная реализация	20	24	36

• С использованием SSE:

Реализация алгоритма	Luffa-256	Luffa-384	Luffa-512
Оригинальная реализация 2009 год
Однопоточная реализация	17	19	30
Томас Оливиера 2010 год
Однопоточная реализация	15	16	24
Многопоточная реализация	15	18	25

Для сравнения, реализация Keccak (победитель конкурса SHA-3 ) в тестах на аналогичном процессоре c использованием SSE показала следующие результаты: Keccak-256 — 15 c/b, Keccak-512 — 12 c/b.

Примечания

Литература

• Hisayoshi Sato, Dai Watanabe, Christophe De Canni`ere. .

• . — С. 19-20 .

• Bart Preneel, Hirotaka Yoshida, Dai Watanabe. .

• Thomaz Oliveira, Julio Lopez. .

Ссылки