Куча (структура данных)
- 1 year ago
- 0
- 0
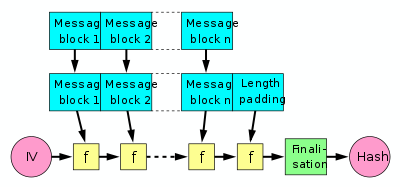
Структура Меркла — Дамгора ( англ. Merkle–Damgård construction , MD ) — метод построения криптографических хеш-функций , предусматривающий разбиение входных сообщений произвольной длины на блоки фиксированной длины и работающий с ними по очереди с помощью функции сжатия, каждый раз принимая входной блок с выходным от предыдущего прохода.
Впервые описана в 1979 году в докторской диссертации Ральфа Меркла . Меркл и независимо показали: если функция сжатия устойчива к коллизиям , то и хеш-функция будет также устойчива — чтобы доказать устойчивость структуры, сообщение дополняется блоком, который кодирует длину первоначального сообщения (упрочнение Меркла — Дамгора).
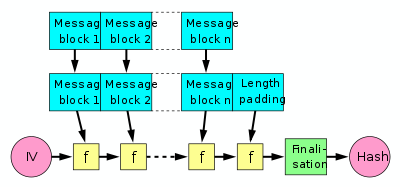
Структура предусматривает вектор инициализации — фиксированное значение, которое зависит от реализации алгоритма, и которое применяется к первому проходу — применению функции сжатия к нему и первому блоку сообщения. Результат каждого прохода передаётся на следующий вход и очередному блоку сообщения; последний блок дополняется нулями, если необходимо, также, добавляется блок с информацией о длине целого сообщения. Для упрочнения хеша последний результат иногда пропускают через функцию финализации ( англ. finalisation function ), которая может использоваться также для уменьшения размера выходного хеша сжатием результата последнего применения в хеш меньшего размера или чтобы гарантировать лучшее смешивание битов и усилить влияние небольшого изменения входного сообщения на хеш (обеспечить лавинный эффект ). Функция финализации часто строится с использованием функции сжатия.
Основные алгоритмы, реализующие структуру Меркла — Дамгора — MD5 , SHA-1 , семейство SHA-2 .
Популярность структуры Меркла — Дамгора обусловлена следующим результатом: если односторонняя функция сжатия устойчива к коллизиям , то и хеш-функция, построенная на её основе, будет также устойчива к коллизиям. При этом структура имеет несколько нежелательных свойств:
Для того, чтобы передать сообщение в функцию сжатия, необходимо дополнить последний блок до полного определёнными данными (обычно нулями). Например, для сообщения « HashInput » и размера блока для функции сжатия 8 байт (64 бит) получится 2 блока:
Но этого недостаточно, так как это будет означать, что различные сообщения, начинающиеся одними и теми же символами, и заканчивающимися нулями или другими байтами из заполнителя, будут поступать в функцию сжатия совершенно одинаковыми блоками, и будет получаться одинаковая хеш-сумма. В этом примере сообщение « HashInput00 » будет разделено на такие же блоки, что и первоначальное сообщение « HashInput ». Чтобы этого избежать, первый бит добавляемых данных должен быть изменён. Так как заполнитель обычно состоит из нулей, первый бит заполнителя должен быть заменён на «1»:
Чтобы усилить хеш, можно добавить длину сообщения в дополнительном блоке:
Чтобы избежать двусмысленности, значение длины сообщения должно быть само по себе устойчиво к добавлению заполнителя в блок. Наиболее распространенные реализации используют фиксированный размер (обычно 64 или 128 бит в современных алгоритмах) и фиксированную позицию в конце последнего блока для кодирования значения длины сообщения.
Однако, немного расточительно кодировать один дополнительный блок для длины сообщения, поэтому существует небольшая оптимизация алгоритма, которая часто используется: если в последнем блоке сообщения достаточно места, значение длины сообщения может быть добавлено к нему. Например, если кодировать длину сообщения в 5 байт, то достаточно двух блоков, для примера:
В 2006 году был предложен подход HAIFA , при котором структура Меркла — Дамгора немного модифицируется: в каждую функцию сжатия дополнительно к блоку сообщения подаётся текущее смещение во входном файле и, опционально, некоторая соль .
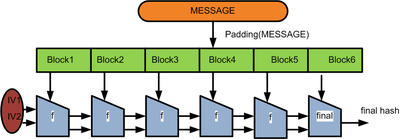
Из-за некоторых слабых мест структуры, особенно проблемы, связанной с дополнением сообщения до необходимой длины, в 2004 году Штефаном Люксом предложено применять широконвейерный хеш ( англ. wilde pipe hash ) , похожий на структуру Меркла — Дамгора, но имеющий больше внутренних состояний, то есть битовая длина, использующаяся внутри алгоритма, больше, чем выходная. Таким образом, последний этап — вторая функция сжатия, которая сжимает последнее внутреннее значение хеша в окончательное значение. SHA-224 и SHA-384 были получены из SHA-256 и SHA-512 , соответственно, путём применения этого алгоритма.