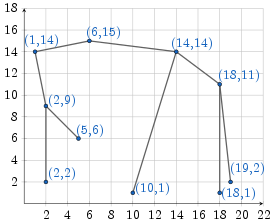
Дека́ртово де́рево , дуча , дерамида ( англ. treap от англ. tree «дерево» + англ. heap «куча») — это структура данных, сочетающая в себе двоичное дерево и двоичную кучу . Хранит пары (x, y) , где для ключа x служит бинарным деревом поиска , а для приоритета y — двоичной кучей.

Декартово дерево впервые было описано Сесилией Арагон и Раймундом Зиделем в 1989.

Свойства

Декартово дерево не является в обычном смысле, и применяют его по следующим причинам:

• Проще реализуется по сравнению, например, с настоящими самобалансирующимися деревьями вроде красно-чёрного .
• Хорошо ведёт себя «в среднем», если ключи y раздать случайно.
• Типичная для сортирующего дерева операция «разделить по ключу x на „меньше x ₀ “ и „не меньше x ₀ “» работает за O ( h ), где h — высота дерева. На красно-чёрных деревьях придётся восстанавливать балансировку и окраску узлов.

Недостатки

• Большие накладные расходы на хранение: вместе с каждым элементом хранятся два-три указателя и случайный ключ y .
• Скорость доступа O ( n ) в худшем, хотя и маловероятном, случае. Поэтому декартово дерево недопустимо, например, в ядрах ОС .

Терминология

В англоязычной литературе декартово дерево, построенное для массива из заданных ключей и присвоенных им при построении случайных весов называется словом-бумажником treap , так как совмещает свойства сортирующего дерева-кучи ( heap ) и случайного двоичного дерева ( tree ) с логарифмическим ожиданием высоты. В русском языке были предложены аналогичные слову treap слова дуча ( дерево + куча ), дерамида ( дерево + пирамида ).

_en использовал для подобной структуры название англ. Cartesian tree — декартово дерево.

Алгоритмы

Простейший алгоритм

Простейший для понимания алгоритм построения декартового дерева по множеству данных пар (x, y) выглядит следующим образом. Упорядочим все пары по ключу x и пронумеруем получившуюся последовательность ключей y:

y(1), y(2), y(3), …, y(n).

Найдём минимальный ключ y. Пусть это будет y(k). Он будет корнем дерева. Ключ y(k) делит последовательность ключей y на две:

y(1), …, y(k−1); y(k+1), …, y(n).

В каждой из них найдём минимальный y — это будут дети узла y(k) — левый и правый. С получившимися 4 кусочками (возможно меньше) поступим аналогичным образом. Предложенный алгоритм построения декартового дерева основан на рекурсии: находим в последовательности минимальный y и назначаем его корнем. Найденный y разбивает последовательность на две части, для каждой из частей запускаем алгоритм построения декартового дерева.

Схематически это можно записать так:

T( y(1), ..., y(n) ) =  root: y(k)   
                           left_tree: T( y(1), ..., y(k−1) )   
                           right_tree: T( y(k+1), ..., y(n)) )
                        where  y(k) = min( y(1), ..., y(n) )

Из данного алгоритма следует, что множество пар (x, y) однозначно определяет структуру декартового дерева. Заметим для сравнения, что множество ключей, которые хранятся в двоичном дереве поиска, не определяют однозначно структуру дерева. То же самое касается двоичной кучи — какова будет структура двоичной кучи (как ключи распределятся по узлам), зависит не только от самого множества ключей, но и от последовательности их добавления. В декартовом дереве такой неоднозначности нет.

Линейный алгоритм

Другой алгоритм построения дерева также основан на рекурсии. Только теперь мы последовательно будем добавлять элементы y и перестраивать дерево. Дерево T(y(1), …, y(k+1)) будет строиться из дерева T(y(1), …, y(k)) и следующего элемента y(k+1).

T( y(1), ..., y(k+1) ) = F ( T( y(1), ..., y(k) ), y(k+1) )

На каждом шаге будем помнить ссылку на последний добавленный узел. Он будет самым правым. Действительно, мы упорядочили ключи y по прикреплённому к ним ключу x. Так как декартово дерево — это дерево поиска, то после проекции на горизонтальную прямую ключи x должны возрастать слева направо. Самый правый узел всегда имеет максимально возможное значение ключа x.

Функция F, которая отображает декартово дерево T(y(1), …, y(k)) предыдущего шага и очередное y(k+1) в новое дерево T(y(1), …, y(k+1)), выглядит следующим образом. Вертикаль для узла y(k+1) определена. Нам необходимо определиться с его горизонталью. Для начала мы проверяем, можно ли новый узел y(k+1) сделать правым ребёнком узла y(k) — это следует сделать, если y(k+1) > y(k). Иначе мы делаем шаг по склону от узла y(k) вверх и смотрим на значение y, которое там хранится. Поднимаемся вверх по склону, пока не найдём узел, в котором значение y меньше, чем y(k+1), после чего делаем y(k+1) его правым ребёнком, а его предыдущего правого ребёнка делаем левым ребёнком узла y(k+1).

Это алгоритм амортизационно (в сумме за все шаги) работает за линейное время (по числу добавляемых узлов). Действительно, как только мы «перешагнули» через какой-либо узел, поднимаясь вверх по склону, то мы его уже никогда не встретим при добавлении следующих узлов. Таким образом, суммарное число шагов вверх по склону не может быть больше общего числа узлов.

Добавление и удаление элементов

Этот раздел статьи ещё не написан . Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. ( 5 июля 2023 )

Добавление и удаление узлов дерева реализуется с помощью операций Merge и Split.

Применение

Этот раздел статьи ещё не написан . Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. ( 5 июля 2023 )

Примечания

Ссылки

Литература

• Raimund Seidel, Cecilia R. Aragon (1996). "Randomized Search Trees". ALGORITHMICA . pp. 540—545.
• Ландовский, Владимир. Структуры данных. — Новосибирский государственный технический университет, 2016. — С. 48—50. — 68 с. — ISBN 978-5-7782-3080-4 .
• Guy E. Blelloch; Margaret Reid-Miller (1998). . Proceedings of the tenth annual ACM symposium on Parallel algorithms and architectures . Puerto Vallarta, Mexico: Association for Computing Machinery. pp. 16—26. doi : . ISBN 0897919890 .

Для улучшения этой статьи желательно : Проставить сноски , внести более точные указания на источники. Оформить статью по правилам . Исправить статью согласно стилистическим правилам Википедии . После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.