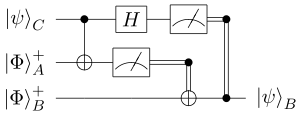
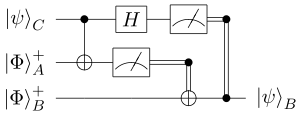
Квантовая схема — модель квантовых вычислений , аналогичная , в которых вычисление представляет собой последовательность квантовых вентилей , измерителей , инициализации кубитов известными значениями и, возможно, других действий. Минимальный набор действий, которые схема должна выполнять над кубитами, чтобы включить квантовые вычисления, известен как .

Схемы построены таким образом, что горизонтальная ось представляет собой время, направленное слева направо. Горизонтальные линии — кубиты , сдвоенные линии — классические биты . Элементы, соединенные этими линиями, — это операции, выполняемые над кубитами, такие как измерения или вентили. Эти линии определяют последовательность событий и обычно не являются физическими проводниками.

Графическое изображение элементов квантовой схемы описано с использованием варианта . Ричард Фейнман использовал раннюю версию нотации квантовой схемы в 1986 году.

Обратимые классические логические вентили

Большинство элементарных логических элементов классического компьютера необратимы. Например, для вентиля И не всегда можно восстановить два входных бита из выходного бита: если выходной бит равен 0, невозможно определить, являются ли входные биты 01, 10 или 00.

Однако обратимые вентили в классических компьютерах легко строятся для битовых строк любой длины; более того, они представляют практический интерес, так как необратимые вентили всегда должны увеличивать физическую энтропию . Обратимый вентиль — это обратимая функция для n -битных данных, которая возвращает n -битные данные, где n -битные данные представляют собой строку битов x ₁ , x ₂ , …, x _n длины n . Набор n -битных данных представляет собой пространство {0,1} ⁿ , которое состоит из 2 ⁿ строк нулей и единиц.

Более точно: n -битный обратимый вентиль — это биективное отображение f из множества {0,1} ⁿ n -битных данных на себя. Примером такого обратимого вентиля f является отображение, применяющее фиксированную перестановку к своим входам. Из соображений практической инженерии обычно изучают вентили только для малых значений n , например, n =1, n =2 или n =3. Эти вентили легко описываются таблицами.

Квантовые логические вентили

Квантовые логические элементы представляют собой обратимые унитарные преобразования по крайней мере на одном кубите. Несколько кубитов, взятые вместе, называются . Чтобы определить квантовые вентили, нам сначала нужно указать квантовую замену n -битных данных. Квантовая версия классического n -битного пространства {0,1} ⁿ является гильбертовым пространством .

${\displaystyle H_{\operatorname {QB} (n)}=\ell ^{2}(\{0,1\}^{n}).}$

По определению это пространство комплекснозначных функций на {0,1} ⁿ и, естественно, пространство внутреннего произведения . ${\displaystyle \ell ^{2}}$ означает, что функция является функцией, . Это пространство также можно рассматривать как состоящее из линейных комбинаций или суперпозиций классических битовых строк. Обратите внимание, что H _{QB( n )} является векторным пространством размерности 2 ⁿ над комплексными числами. Элементы этого векторного пространства являются возможными векторами состояния n - кубитных .

Используя кет-нотацию Дирака, если x ₁ , x ₂ , …, x _n — классическая битовая строка, то

${\displaystyle |x_{1},x_{2},\cdots ,x_{n}\rangle \quad }$

это специальный n -кубитный регистр, соответствующий функции, которая отображает эту классическую битовую строку в 1 и отображает все остальные битовые строки в 0; эти 2 ⁿ специальных n -кубитных регистров называются вычислительными базисными состояниями . Все n -кубитные регистры представляют собой сложные линейные комбинации этих вычислительных базовых состояний.

Квантовые логические вентили, в отличие от классических логических вентилей, всегда обратимы. Требуется особый вид обратимой функции, а именно унитарное отображение, то есть линейное преобразование комплексного пространства с внутренним произведением , которое сохраняет эрмитово внутреннее произведение . n -кубитный (обратимый) квантовый вентиль представляет собой унитарное отображение U из пространства H _{QB( n )} n -кубитных регистров на себя.

Как правило, нас интересуют вентили только для небольших значений n .

Обратимый n -битный классический логический элемент порождает обратимый n -битный квантовый элемент следующим образом: каждому обратимому n -битному логическому элементу f соответствует квантовый элемент Wf , определяемый следующим образом:

${\displaystyle W_{f}(|x_{1},x_{2},\cdots ,x_{n}\rangle )=|f(x_{1},x_{2},\cdots ,x_{n})\rangle .}$

Обратите внимание, что W _f переставляет вычислительные базисные состояния.

Особое значение имеет управляемый вентиль НЕ (также называемый вентилем CNOT ) W _CNOT , определённый на квантованных 2 кубитах. Другими примерами квантовых логических вентилей, производных от классических, являются вентиль Тоффоли и вентиль Фредкина .

Однако структура кубитов в гильбертовом пространстве допускает множество квантовых вентилей, которые не индуцируются классическими вентилями. Например, относительный фазовый сдвиг — это вентиль размером 1 кубит, заданный умножением на оператор фазового сдвига :

${\displaystyle P(\varphi )={\begin{bmatrix}1&0\\0&e^{i\varphi }\end{bmatrix}},}$

так что

${\displaystyle P(\varphi )|0\rangle =|0\rangle \quad P(\varphi )|1\rangle =e^{i\varphi }|1\rangle .}$

Обратимые логические схемы

Снова рассмотрим первое обратимое классическое вычисление. Концептуально нет никакой разницы между обратимой n -битной схемой и обратимым n -битным логическим элементом: любой из них является просто обратимой функцией в пространстве n -битных данных. Однако, как упоминалось в предыдущем разделе, по техническим причинам мы хотели бы иметь небольшое количество простых обратимых вентилей, из которых можно собрать любую обратимую схему.

Чтобы объяснить этот процесс сборки, предположим, что у нас есть обратимый n -битовый вентиль f и обратимый m -битовый вентиль g . Соединение их вместе означает создание новой схемы путем соединения некоторого набора из k выходов f с некоторым набором из k входов g , как показано на рисунке ниже. На этом рисунке n = 5, k = 3 и m = 7. Полученная схема также обратима и работает с n + m − k битами.

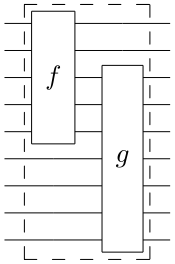
Мы будем называть эту схему классической сборкой (это понятие соответствует техническому определению в пионерской статье Китаева , цитируемой ниже). При составлении этих обратимых машин важно обеспечить, чтобы промежуточные машины также были обратимыми. Это условие гарантирует, что промежуточный «мусор» не будет создан (чистым физическим эффектом будет увеличение энтропии).

Обратите внимание, что каждая горизонтальная линия на картинке выше представляет либо 0, либо 1, а не эти вероятности. Поскольку квантовые вычисления обратимы, на каждом «шаге» количество строк должно совпадать с количеством входных строк. Кроме того, каждая входная комбинация должна быть сопоставлена с одной комбинацией на каждом «шаге». Это означает, что каждая промежуточная комбинация в квантовой схеме является биективной функцией входа.

Теперь можно показать, что вентиль Тоффоли являются универсальным вентилем . Это означает, что для любой обратимой классической n -битной схемы h мы можем построить классическую сборку вентилей Тоффоли вышеописанным способом, чтобы создать ( n + m )-битную схему f такую, что

${\displaystyle f(x_{1},\ldots ,x_{n},\underbrace {0,\dots ,0} )=(y_{1},\ldots ,y_{n},\underbrace {0,\ldots ,0} )}$

где в скобках имеется m нулевых входов и

${\displaystyle (y_{1},\ldots ,y_{n})=h(x_{1},\ldots ,x_{n})}$ .

Обратите внимание, что конечный результат всегда содержит строку из m нулей в качестве вспомогательных битов. Никакого «мусора» никогда не производится, так что это вычисление действительно в физическом смысле не генерирует энтропию. Этот вопрос подробно рассмотрен в статье Китаева.

В более общем смысле любая функция f (биективная или нет) может быть смоделирована схемой вентилей Тоффоли. Очевидно, что если отображение не является инъективным , в какой-то момент симуляции (например, на последнем шаге) должен быть создан некоторый «мусор».

Для квантовых схем можно определить аналогичный состав вентилей кубита. То есть связанный с любой классической сборкой, как указано выше, мы можем создать обратимую квантовую схему, когда вместо f у нас есть n -кубитовый вентиль U , а вместо g у нас есть m -кубитовый вентиль W. См. иллюстрацию ниже:

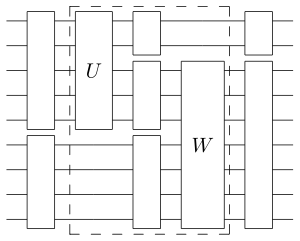
Тот факт, что соединение вентилей таким образом приводит к унитарному отображению в пространстве n + m − k кубитов, легко проверить. В реальном квантовом компьютере физическая связь между вентилями является серьёзной инженерной задачей, поскольку это одно из мест, где может возникнуть декогерентность .

Существуют также теоремы универсальности для некоторых наборов хорошо известных вентилей; такая теорема универсальности существует, например, для пары, состоящей из упомянутого выше однокубитного фазового вентиля U _θ (для подходящего значения θ) вместе с двухкубитным вентилем CNOT W _CNOT . Однако теорема универсальности для квантового случая несколько слабее, чем для классического; он утверждает только, что любая обратимая n -кубитная схема может быть сколь угодно хорошо аппроксимирована схемами, собранными из этих двух элементарных вентилей. Обратите внимание, что существует бесчисленное множество возможных однокубитных фазовых вентилей, по одному на каждый возможный угол θ, поэтому все они не могут быть представлены конечной схемой, построенной из { U _θ , W _CNOT }.

Квантовые вычисления

До сих пор мы не показывали, как квантовые схемы используются для выполнения вычислений. Поскольку многие важные численные задачи сводятся к вычислению унитарного преобразования U в конечномерном пространстве (ярким примером является знаменитое дискретное преобразование Фурье ), можно было бы ожидать, что некоторая квантовая схема может быть разработана для выполнения преобразования U . В принципе, нужно только подготовить состояние n кубитов ψ как подходящую суперпозицию вычислительных базисных состояний для входа и измерить выход U ψ. К сожалению, здесь есть две проблемы:

• Нельзя измерить фазу ψ ни в каком вычислительном базовом состоянии, поэтому нет возможности прочитать полный ответ. Такова природа измерения в квантовой механике .
• Невозможно эффективно подготовить входное состояние ψ.

Это не мешает использовать квантовые схемы для дискретного преобразования Фурье в качестве промежуточных шагов в других квантовых схемах, но их использование более тонкое. На самом деле квантовые вычисления являются вероятностными .

Теперь мы предоставим математическую модель того, как квантовые схемы могут имитировать вероятностные , но классические вычисления. Рассмотрим r -кубитную схему U с пространством регистров H _{QB( r )} . Таким образом, U является унитарным отображением

${\displaystyle H_{\operatorname {QB} (r)}\rightarrow H_{\operatorname {QB} (r)}.}$

Чтобы связать эту схему с классическим отображением на битовых цепочках, мы определяем

• Входной регистр X = {0,1} ^m из m (классических) бит.
• Выходной регистр Y = {0,1} ⁿ из n (классический) бит.

Содержимое x = x ₁ , …, x _m классического регистра ввода используется для инициализации регистра кубита каким-то образом. В идеале это должно быть сделано с вычислительным базисным состоянием

${\displaystyle |{\vec {x}},0\rangle =|x_{1},x_{2},\cdots ,x_{m},\underbrace {0,\dots ,0} \rangle ,}$

где имеется r - m подчеркнутых нулевых входов. Тем не менее, эта идеальная инициализация совершенно нереалистична. Поэтому предположим, что инициализация представляет собой смешанное состояние, заданное некоторым оператором плотности S , который находится вблизи идеализированного входа в некоторой подходящей метрике, например

${\displaystyle \operatorname {Tr} \left({\big |}|{\vec {x}},0\rangle \langle {\vec {x}},0|-S{\big |}\right)\leq \delta .}$

Точно так же пространство выходного регистра связано с регистром кубита наблюдаемой величиной A со значением Y . Обратите внимание, что наблюдаемые в квантовой механике обычно определяются в терминах проекционнозначных мер на R ; если переменная оказывается дискретной, то проекционнозначная мера сводится к семейству {E _λ }, индексированному некоторым параметром λ, ранжирующимся на счетном множестве. Точно так же наблюдаемая со значением Y может быть связана с семейством попарно ортогональных проекций {E _y }, индексированных элементами Y , такими, что

${\displaystyle I=\sum _{y\in Y}\operatorname {E} _{y}.}$

Данному смешанному состоянию S соответствует вероятностная мера на Y , заданная выражением

${\displaystyle \operatorname {Pr} \{y\}=\operatorname {Tr} (S\operatorname {E} _{y}).}$

Функция F : X → Y вычисляется схемой U : H _{QB( r )} → H _{QB( r )} с точностью до ε тогда и только тогда, когда для всех битовых цепочек x длины m

${\displaystyle \left\langle {\vec {x}},0{\big |}U^{*}\operatorname {E} _{F(x)}U{\big |}{\vec {x}},0\right\rangle =\left\langle \operatorname {E} _{F(x)}U(|{\vec {x}},0\rangle ){\big |}U(|{\vec {x}},0\rangle )\right\rangle \geq 1-\epsilon .}$

Тогда

${\displaystyle \left|\operatorname {Tr} (SU^{*}\operatorname {E} _{F(x)}U)-\left\langle {\vec {x}},0{\big |}U^{*}\operatorname {E} _{F(x)}U{\big |}{\vec {x}},0\right\rangle \right|\leq \operatorname {Tr} ({\big |}|{\vec {x}},0\rangle \langle {\vec {x}},0|-S{\big |})\|U^{*}\operatorname {E} _{F(x)}U\|\leq \delta }$

так что

${\displaystyle \operatorname {Tr} (SU^{*}\operatorname {E} _{F(x)}U)\geq 1-\epsilon -\delta .}$

Теорема . Если ε + δ < 1/2, то распределение вероятностей

${\displaystyle \operatorname {Pr} \{y\}=\operatorname {Tr} (SU^{*}\operatorname {E} _{y}U)}$

на Y можно использовать для определения F ( x ) со сколь угодно малой вероятностью ошибки путем мажоритарной выборки для достаточно большого объёма выборки. В частности, возьмите k независимых выборок из распределения вероятностей Pr на Y и выберите значение, с которым согласуется более половины выборок. Вероятность того, что значение F ( x ) выбрано более чем k /2 раз, составляет не менее

${\displaystyle 1-e^{-2\gamma ^{2}k},}$

где γ = 1/2 — ε — δ.

Это следует из применения границы Чернова .

См. также

• и BQP
• использует
• Спиновые сети

Примечания

Литература

• ; Brassard, Gilles ; Kenigsberg, Dan; Mor, Tal (2004), "Quantum computing without entanglement", Theoretical Computer Science , 320 (1): 15—33, arXiv : , doi : .
• ; ; Larsen, Michael J.; Wang, Zhenghan (2003), "Topological quantum computation", Bulletin of the American Mathematical Society , 40 (1): 31—38, arXiv : , doi : {{ citation }} : Указан более чем один параметр |author1-link= and |author-link= ( справка ) .
• Hirvensalo, Mika (2001), Quantum Computing , ISBN 3-540-66783-0 .
• Kitaev, A. Yu. (1997), "Quantum computations: algorithms and error correction", Uspekhi Mat. Nauk , 52 (6(318)): 53—112, doi : .
• ; Chuang, Isaac L. (2000), Quantum Computation and Quantum Information , ISBN 0-521-63235-8 .

Ссылки

• — это пакет макросов для рисования схем квантовых цепей в LaTeX.
• — браузерный редактор и симулятор квантовых схем.
• — среда квантовых сценариев на основе браузера.
• — браузерный редактор и симулятор квантовых схем.