Interested Article - Гипербола Киперта

- 2020-06-20
- 1

Гипе́рбола Ки́перта — гипербола , определяемая по данному треугольнику . Если последний представляет собой треугольник общего положения, то эта гипербола является единственным коническим сечением, проходящим через его вершины, ортоцентр и центроид .
Определение через изогональное сопряжение
Гипербола Киперта — кривая, изогонально сопряжённая прямой, проходящей через точку Лемуана и центр описанной окружности данного треугольника.
- Прямая, проходящая через центр описанной окружности и точку Лемуана , называется осью Брокара . На ней лежат точки Аполлония . Иначе говоря, гипербола Киперта — кривая, изогонально сопряжённая оси Брокара данного треугольника.
Определение через треугольники в трилинейных координатах
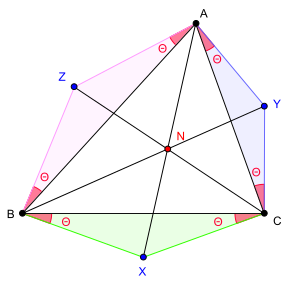
Определение через треугольники в трилинейных координатах :
- Если три треугольника , и построены на сторонах треугольника , являются подобными , равнобедренными с основаниями на сторонах исходного треугольника, и одинаково расположенными (то есть все они построены либо с внешней стороны, либо с внутренней стороны), то прямые , и пересекаются в одной точке . Тогда гипербола Киперта может быть определена виде геометрического места точек (см. рис.).
Если общий угол при основании равен , то вершины трёх треугольников имеют следующие трилинейные координаты:
Трилинейные координаты произвольной точки N, лежащей на гиперболе Киперта
- .
Уравнение гиперболы Киперта в трилинейных координатах
Геометрическое место точек при изменении угла при основании треугольников между и является гиперболой Киперта с уравнением
- ,
где , , — трилинейные координаты точки в треугольнике.
Известные точки, лежащие на гиперболе Киперта
Среди точек, лежащих на гиперболе Киперта, имеются такие важные точки треугольника :
| Значение | Точка |
|---|---|
| , центроид треугольника (X2) | |
| (или ) | , ортоцентр треугольника (X4) |
| Центр Шпикера (X10) | |
| Внешняя точка Вектена (Vecten points) (X485) | |
| Внутренняя точка Вектена (Vecten points) (X486) | |
| , первая точка Наполеона (X17) | |
| , вторая точка Наполеона (X18) | |
| , первая точка Ферма (X13) | |
| , вторая точка Ферма (X14) | |
|
(если
)
(если ) |
Вершина |
|
(если
)
(если ) |
Вершина |
|
(если
)
(если ) |
Вершина |
Перечень точек, лежащих на гиперболе Киперта
Гипербола Киперта проходит через следующие центры треугольника X(i) :
- для i=2, ( Центроид треугольника ),
- i=4 ( Ортоцентр ),
- i=10 ( Центр Шпикера ; то есть, инцентр треугольника с вершинами в серединах сторон данного треугольника ABC ),
- i=13 (первая точка Ферма ), i=14 (вторая точка Ферма ),
- i=17 ( первая точка Наполеона ), i=18 ( вторая точка Наполеона ),
- i=76 (третья точка Брокара ),
- i=83 (точка, изогонально сопряжённая серединной точке между точками Брокара ),
- i=94, 96,
- i=98 ( Точка Тарри =Tarry point),
- i=226, 262, 275, 321,
- i=485 ( Внешняя точка Вектена ), i=486 ( Внутренняя точка Вектена ),
- i=598, 671, 801, 1029, 1131, 1132,
- i=1139 (внутренняя точка пятиугольника=inner pentagon point), i=1140 (внешняя точка пятиугольника=outer pentagon point),
- i=1327, 1328, 1446, 1676, 1677, 1751, 1916, 2009, 2010, 2051, 2052, 2394, 2592, 2593,
- i=2671 (первая точка золотого арбелоса=first golden arbelos point),
- i=2672 (вторая точка золотого арбелоса=second golden arbelos point),
- i=2986, 2996
Обобщение теоремы Лестера в виде теоремы Б. Гиберта (2000)
Теорема Б. Гиберта (2000) обобщает теорему об окружности Лестера , а именно: любая окружность, диаметр которой является хордой гиперболы Киперта треугольника и перпендикулярен его прямой Эйлера , проходит через точки Ферма .
История
Название данная гипербола получила в честь открывшего её немецкого математика Фридриха Вильгельма Августа Людвига Киперта (Friedrich Wilhelm August Ludwig Kiepert, 1846—1934) .
Свойства
- Гипербола Киперта — равносторонняя или равнобочная (то есть её асимптоты перпендикулярны), следовательно, её центр, обозначенный в энциклопедии центров треугольника как Х(115), лежит на окружности Эйлера .
См. также
Примечания
- ↑ , p. 188—205.
- Акопян А. В. , Заславский А. А. . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 125—126.
- ↑ Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- B. Gibert (2000): [ Message 1270] . Entry in the Hyacinthos online forum, 2000-08-22. Accessed on 2014-10-09.
- Paul Yiu (2010), от 7 октября 2021 на Wayback Machine . Forum Geometricorum, volume 10, pages 175—209. MR :
Литература
- Eddy R. H., Fritsch R. . The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle // Math Magazine , 1994, 67 . — P. 188—205.
- 2020-06-20
- 1
































![{\displaystyle \operatorname {arctg} [\operatorname {tg} (A/2)\operatorname {tg} (B/2)\operatorname {tg} (C/2)]}](/images/005/359/5359819/35.jpg?rand=811640)