Interested Article - Кривая Осгуда
- 2021-10-23
- 1
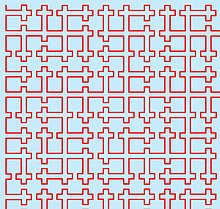

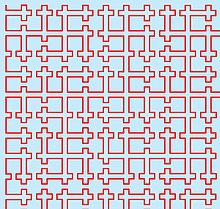
В математике кривая Осгуда — это самонепересекающаяся кривая ( кривая или дуга Жордана) с положительной площадью . Более формально, это кривые на евклидовой плоскости с положительной двумерной мерой Лебега .
Истории
Первые примеры таких кривых были найдены Вильямом Фогом Осгудом и Лебегом . Оба примера имеют положительную площадь в некоторых частях кривых, но нулевую площадь в других частях. Этот недостаток была исправлен Кноппом , который нашёл кривую, имеющую положительную площадь вблизи каждой её точки, основываясь на более ранних построениях Вацлава Серпинского . Пример Кноппа имеет дополнительные преимущества в том, что при построении площадь может составлять любую часть площади выпуклой оболочки .
Фрактальное построение
Хотя большинство заполняющих пространство кривых не являются кривыми Осгуда (они имеют положительную площадь, но, зачастую, бесконечное число раз пересекают себя, что нарушает определение кривой Жордана), можно модифицировать рекурсивное построение заполняющих пространство кривых или фрактальных кривых, чтобы получить кривую Осгуда .
Первоначально Осгуд в своей публикации 1903 года рассмотрел кривую, заполняющую квадрат . Именно эта ломаная получила его имя . Позже это название было обобщено и на другие фигуры. Например, построение Кноппа использует рекурсивное разделение треугольников на пары меньших треугольников, имеющих общую вершину, путём удаления клиньев. Если удаляемые клинья на каждом уровне построения составляют не меняющуюся (дробную) часть площади треугольников, в результате получим фрактал Чезаро, подобный кривой Коха , но при удалении клиньев, площади которых уменьшаются быстрее, получаем кривую Осгуда .
Построение Данжуа — Риса
Другой путь построения кривой Осгуда — это использование двумерной версии , полностью разъединённого множества точек с ненулевой площадью, к которой применяется , согласно которой любое ограниченное и вполне несвязное подмножество плоскости является подмножеством жордановой кривой .
См. также
Примечания
- ↑ Слюсар, В. Электроника: наука, технология, бизнес. — 2007. — № 6. С. 86 - 87. (2007). Дата обращения: 27 апреля 2020. 3 апреля 2018 года.
- .
- .
- .
- .
- ↑ ; , Секция 8.3, Кривые Осгуда Серпинского и кноппа, от 29 мая 2016 на Wayback Machine .
- ; ; ).
- William F. Osgood . A Jordan Curve of Positive Area // Transactions of the American Mathematical Society . — 1903. — Т. 4 . — С. 107–112 . — ISSN . — doi : . — .
- .
Литература
- M. Balcerzak, A. Kharazishvili. On uncountable unions and intersections of measurable sets // Georgian Mathematical Journal. — 1999. — Т. 6 , вып. 3 . — С. 201–212 . — doi : . .
- K. Knopp. Einheitliche Erzeugung und Darstellung der Kurven von Peano, Osgood und von Koch // Archiv der Mathematik und Physik. — 1917. — Т. 26 . — С. 103–115 .
- Timothy Lance, Edward Thomas. // American Mathematical Monthly . — 1991. — Т. 98 , вып. 2 . — С. 124–127 . — doi : .
- H. Lebesgue . Sur le problème des aires (фр.) // Bulletin de la Société Mathématique de France. — 1903. — Vol. 31 . — P. 197–203 .
- William F. Osgood . A Jordan Curve of Positive Area // Transactions of the American Mathematical Society . — 1903. — Т. 4 . — С. 107–112 . — ISSN . — doi : . — .
- Tibor Radó. Length and Area. — American Mathematical Society, New York, 1948. — С. 157. — (American Mathematical Society Colloquium Publications, vol. 30).
- Hans Sagan. // The Mathematical Intelligencer . — 1993. — Т. 15 , вып. 4 . — С. 37–43 . — doi : .
- Hans Sagan. Space-filling curves. — Springer-Verlag, 1994. — (Universitext). — ISBN 0-387-94265-3 . — doi : .
Ссылки
- Robert Dickau. Knopp's Osgood Curve Construction. — Wolfram Demonstrations Project, 2013.
- 2021-10-23
- 1





















