Interested Article - Правило ненулевого индекса

Кривая (сверху) заполнена согласно двум правилам: Правило чётный-нечётный (слева), и **правило ненулевого индекса** (справа). В обоих случаях стрелка показывает луч из точки P, направленный вовне кривой. В случае правила чётный-нечётный, луч пересекается двумя линиями, чётным числом, так что P считается 'вне' кривой. Согласно правилу ненулевого индекса, луч пересекается в направлении часовой стрелки дважды, каждое даёт −1 в индекс, так что всего получим −2, ненулевое число, и P считается 'внутри' кривой.

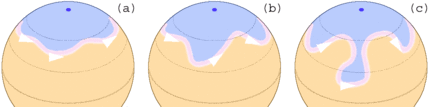
В двумерной компьютерной графике , правило ненулевого индекса означает способ определения, лежит ли точка внутри замкнутой кривой. В отличие от похожего правила чётный-нечётный , этот алгоритм полагается на знание направления движения для каждой части кривой.

Для заданной кривой C и заданной точки P построим луч (прямую линию), направленный из точки P в любом направлении в бесконечность. Найдём все пересечения C с этим лучом. Считаем индекс точки следующим образом: для любого пересечения в направлении движения часовой стрелки (кривая, проходит через луч слева направо, если смотреть из точки P) вычитаем 1, для любого пересечения против часовой стрелки (кривая проходит справа налево, если смотреть из точки P) прибавляем 1. Если полный индекс точки равен нулю, P находится вне C, в противном случае точка находится внутри.

Индекс точки эффективно вычисляет, сколько полных оборотов против часовой стрелки кривая делает вокруг точки P. (Если бы P была гвоздём, а C была бы завязанным в кольцо куском нитки, вытягивание какой-то части нитки прочь от гвоздя приведёт либо к вытягиванию всей нитки, либо нитка окажется накрученной несколько раз на гвоздь.) Некоторые реализации считают число проходов по часовой стрелке, так что при проходе по часовой стрелке добавляется 1, а против часовой стрелки вычитается 1. Результат будет тем же самым.

Формальное определение индекса точки P по отношению к кривой C (где P не лежит на кривой) следующее:

Положим, что точка Q проходит по кривой C. Конец вектора из P в Q, после нормализации движется по единичной окружности с центром в P. Индекс точки — это число оборотов конца вектора.

Компьютерная векторная графика SVG имеет возможности, позволяющие использовать правило ненулевого индекса при рисовании многоугольников.

См. также

Примечания

James D. Foley, Andries Van Dam, Steven K. Feiner & John F. Hughes. Computer Graphics: Principles and Practice. — Addison-Wesley, 1996. — С. 965. — ISBN 9780201848403 .
от 28 октября 2014 на Wayback Machine , w3c.org, retrieved 2012 12 30