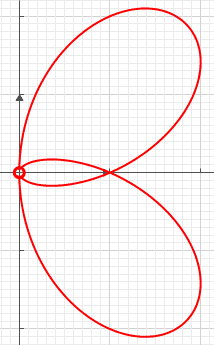
В точка самосоприкосновения ( англ. tacnode ) или двойной касп — вид особой точки . Определяется как точка, где две (или более) соприкасающиеся кривой окружности в этой точке касаются . Это означает, что две ветви кривой имеют одну и ту же касательную в двойной точке .

Каноническим примером служит кривая

${\displaystyle (y-x^{2})(y+x^{2})=0.}$

Другой пример точки самоприкосновения — кривая, показанная на рисунке и имеющая уравнение

${\displaystyle (x^{2}+y^{2}-3x)^{2}-4x^{2}(2-x)=0.}$

Некоторые обобщения

Рассмотрим гладкую , принимающую вещественные значения функцию двух переменных, скажем, f ( x , y ), где x и y — вещественные числа . Таким образом, f отображает плоскость в прямую. На пространство всех таких гладких функций действует группа диффеоморфизмов плоскости и диффеоморфизмов прямой, то есть диффеоморфизмы меняют координаты как в области определения , так и в области значений . Это действие разбивает всё на классы эквивалентности , то есть орбиты действия группы.

Одно такое семейство классов эквивалентности обозначается , где k — неотрицательное целое. Обозначение ввёл В. И. Арнольд . Говорят, что функция f имеет особенность типа , если она лежит на орбите x ² ± y ^{k +1} , то есть существует диффеоморфическое преобразование координат в области определения и в области значений, которое переводит f в одну из этих форм. Говорят, что эти простые формы x ² ± y ^{k +1} задают нормальные формы для особенностей типа .

Кривая с уравнением f = 0 будет иметь в начале координат точку самоприкосновения тогда и только тогда, когда f имеет особенность типа A ₃ ⁻ в начале координат.

Заметим, что точка самопересечения кривой ( x ² − y ² = 0) соответствует A ₁ ⁻ -особенности. Точка самоприкосновения соответствует A ₃ ⁻ -особенности. Фактически, любая особенность типа A _{2 n +1} ⁻ , где n ≥ 0 — целое число, соответствует кривой с самопересечением. С увеличением порядок самопересечения увеличивается — поперечное пересечение, простое касание, и так далее.

Особенности типа A _{2 n +1} ⁺ для действительных чисел не представляют интереса — все они соответствуют изолированным точкам. В комплексных числах особенности A _{2 n +1} ⁺ и A _{2 n +1} ⁻ эквивалентны — ( x , y ) → ( x , iy ) даёт требуемый диффеоморфизм нормальных форм.

См. также

• Изолированная точка кривой
• Касп или Точка возврата

Примечания

Литература

• Е. В. Шикин, М. М.Франк-Каменцкий. Пункт 18. Особые точки кривых // . — М. : Фазис, 1997. — С. . — ISBN 5-7036-0027-8 .
• Ю. А. Аминов. 9. Особые точки плоских кривых // Дифференциальная геометрия и топология кривых. — М. : Наука, 1987. — С. 38—39.

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .