Interested Article - Эквихордный центр
- 2020-01-08
- 1
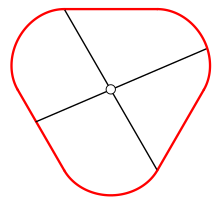
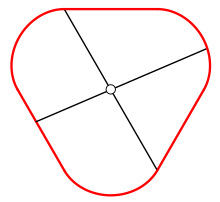
Эквихордный центр — точка внутри плоской кривой, такая, что все хорды , проходящие через неё, равны. Кривые, имеющие эквихордный центр, называются эквихордными .
Примеры
Эквихордными кривыми являются
- Окружности , центр окружности является её эквихордным центром.
-
Подера
на
кривой постоянной ширины
относительно точки
внутри кривой. При этом
является её эквихордным центром.
- В частности, для окружности получаем улитку Паскаля .
Свойства
-
Любая выпуклая кривая имеет не более одного эквихордного центра.
- То, что выпуклая кривая не может иметь трёх центров, было доказано Фудзиварой в 1916 году; он же сформулировал задачу о том, что двух тоже быть не может. Задача была независимо сформулирована Вильгельмом Бляшке , и в 1917 году и решена в 1997-м. Его доказательство довольно сложное, оно занимает 72 страницы и использует комплексный анализ и алгебраическую геометрию .
Литература
- W. Blaschke, W. Rothe, and R. Weitztenböck. Aufgabe 552. Arch. Math. Phys., 27:82, 1917
- M. Fujiwara. Über die Mittelkurve zweier geschlossenen konvexen Curven in Bezug auf einen Punkt. Tôhoku Math J., 10:99-103, 1916
- Marek R. Rychlik (1997), «A complete solution to the equichordal point problem of Fujiwara, Blaschke, Rothe and Weitzenböck», Inventiones Mathematicae 129 (1): 141—212
- Steven G. Krantz (1997), Techniques of Problem Solving, American Mathematical Society,
- 2020-01-08
- 1




