Interested Article - Компланарность
- 2021-10-11
- 1
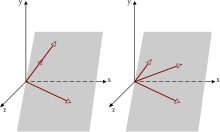
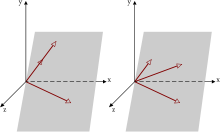
Компланарность ( лат. com — совместность, лат. planus — плоский, ровный) — свойство трёх (или большего числа) векторов , которые, будучи приведёнными к общему началу, лежат в одной плоскости .
Свойства
Если хотя бы один из трёх векторов — нулевой, то три вектора тоже считаются компланарными. Тройка векторов, содержащая пару коллинеарных векторов, компланарна.
Смешанное произведение компланарных векторов равно нулю, это свойство — основной критерий компланарности трёх векторов. Эквивалентный критерий компланарости — линейная зависимость компланарных векторов: существуют действительные числа и такие, что для компланарных , и за исключением случаев или .
В трёхмерном пространстве три некомпланарных вектора , и образуют базис . То есть любой вектор можно представить в виде: . Тогда будут координатами в данном базисе.
Обобщения
Критерии компланарности позволяют определить это понятие для векторов, понимаемых не в геометрическом смысле, а, например, как элементы произвольного векторного пространства .
Иногда компланарными называют те точки (или другие объекты), которые лежат на (принадлежат) одной плоскости . 3 точки определяют плоскость и, тем самым, всегда (тривиально) компланарны. 4 точки, в общем случае (в общем положении ), некомпланарны.
Можно распространить понятие компланарности и на прямые в пространстве. Тогда параллельные или пересекающиеся прямые будут компланарны, а скрещивающиеся прямые — нет.
Примечания
- Выгодский М. Я. Справочник по высшей математике. М., Наука, 1975, § 115
- 2021-10-11
- 1














