Оптимальны́й приём сигна́лов — область радиотехники , в которой обработка принимаемых сигналов осуществляется на основе методов математической статистики .

История

По мнению на возможность использования статистических методов в радиотехнике, по-видимому впервые, непосредственно указали работы А. Н. Колмогорова и Н. Винера по синтезу оптимальных линейных фильтров . В 1946 году В. А. Котельников в своей диссертации впервые сформулировал задачи оценки оптимальных параметров сигналов на фоне аддитивного гауссовского шума и нашёл их решения. В середине 1950-х годов были решены некоторые задачи оптимального приёма сигналов в каналах с флуктуационным шумом, неопределённой фазой и рэлеевскими замираниями .

В конце 1950-х и начале 1960-х годов стали развиваться

• оптимальные методы приёма стохастических пространственно-временных сигналов
• оптимальные методы приёма в каналах с флуктуационным шумом и селективными замираниями по частоте и времени

До начала 1960-х годов методы оптимальной обработки сигналов разрабатывались применительно к задачам радиотехники , в первую очередь касающимся радиолокации и связи. После методы оптимальной обработки стали применяться также и в других предметных областях, в частности гидроакустике , где помехи имеют более сложную структуру, чем в радиолокации. Кроме того, среда распространения гидроакустических колебаний существенно неоднородна. В результате развития теории оптимальной обработки сигналов с учётом гидроакустической специфики сформировалась теория оптимальной обработки гидроакустических сигналов, учитывающая неоднородный характер гидроакустической среды распространения колебаний и сложный характер помеховой обстановки.

Примерно с 1970-х годов начинали развиваться методы совместного различения сигналов и оценивания их параметров

Задачи

Задачами теории оптимального приёма сигналов являются обнаружение сигнала , , , , и распознавание образов . Для их описания допустим, что принимаемый сигнал ${\displaystyle r(t)}$ представляет собой сумму сигнала ${\displaystyle s(t,\lambda )}$ и аддитивной помехи ${\displaystyle n(t)}$ :

${\displaystyle r(t)=s(t,\lambda )+n(t)}$ ,

где ${\displaystyle \lambda }$ — параметр сигнала ${\displaystyle s(t,\lambda )}$ , который в общем случае является векторным , ${\displaystyle n(t)}$ — аддитивный белый гауссовский шум .

Используя это предположение, основные задачи теории оптимального приёма сигналов можно описать следующим образом.

Обнаружение сигнала

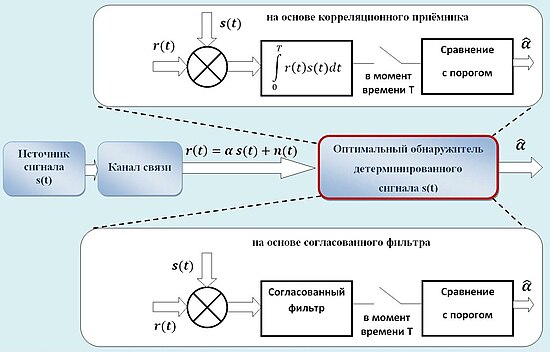
Допустим, что в принятом сигнале ${\displaystyle r(t)}$ может присутствовать или отсутствовать сигнал ${\displaystyle s(t,\lambda )}$ , то есть принимаемый сигнал ${\displaystyle r(t)}$ равен ${\displaystyle r(t)=\alpha s(t,\lambda )+n(t)}$ , где случайная величина ${\displaystyle \alpha }$ может принимать значения 0 (сигнал отсутствует) или 1 (сигнал присутствует); ${\displaystyle s(t,\lambda )}$ — наблюдаемый на интервале наблюдения [0, T] . При решении задачи обнаружении сигнала необходимо определить наличие сигнала ${\displaystyle s(t,\lambda )}$ в ${\displaystyle r(t)}$ , то есть оценить значение параметра ${\displaystyle \alpha }$ . При этом возможны два варианта. Априорные данные — вероятности ${\displaystyle p_{p}}$ ${\displaystyle _{r}(t,\alpha =0)}$ и ${\displaystyle p_{p}}$ ${\displaystyle _{r}(t,\alpha =1)}$ — могут быть известны или нет.

Сформулированная задача обнаружения сигнала является частным случаем общей задачи статистической проверки гипотез . Гипотезу об отсутствии сигнала будем обозначать ${\displaystyle H_{0}}$ , а гипотезу о наличии сигнала — ${\displaystyle H_{1}}$ .

Если априорные вероятности ${\displaystyle P_{pr}(H_{0})}$ и ${\displaystyle P_{pr}(H_{1})}$ известны, то можно использовать критерий минимума среднего риска (байесовский критерий) ${\displaystyle R}$ :

${\displaystyle R=\sum _{i,k=0}^{1}P_{pr}(H_{i})Q_{ik}\int \limits _{X_{k}}W(x|H_{i})dx}$ ,

где { ${\displaystyle Q_{ik}}$ } — матрица потерь , а ${\displaystyle W(x|H_{i})}$ — функция правдоподобия выборки наблюдаемых данных, если предполагается истинность гипотезы ${\displaystyle H_{i}}$ .

В этом случае, если априорные вероятности ${\displaystyle P_{pr}(H_{0})}$ и ${\displaystyle P_{pr}(H_{1})}$ неизвестны, то с пороговым значением ${\displaystyle h_{0}}$ сравнивается отношение правдоподобия ${\displaystyle l_{0}}$ :

${\displaystyle l_{0}={\frac {F(r|H_{1})}{F(r|H_{0})}}=exp({\frac {2}{N}}\int \limits _{0}^{T}r(t)s(t)dt-E/N)}$ ,

где E — энергия сигнала, а N — односторонняя спектральная плотность гауссовского аддитивного белого шума . Если ${\displaystyle l_{0}>h_{0}}$ , то принимаете гипотеза о наличии сигнала, иначе о его отсутствии на интервале наблюдения [ ${\displaystyle 0,T}$ ].

Если априорные вероятности ${\displaystyle P(H_{0})}$ и ${\displaystyle P(H_{1})}$ известны, то решение о наличии сигнала принимается на основе сравнения отношения апостериорных вероятностей ${\displaystyle l_{1}}$ с некоторым пороговым значением ${\displaystyle h_{1}}$ :

${\displaystyle l_{1}={\frac {P_{ps}(H_{1})}{P_{ps}(H_{0})}}={\frac {P_{pr}(H_{1})}{P_{pr}(H_{0})}}exp({\frac {2}{N}}\int \limits _{0}^{T}r(t)s(t)dt-E/N)}$ .

Если ${\displaystyle l_{1}>h_{1}}$ , то принимаете гипотеза о наличии сигнала, иначе о его отсутствии на интервале наблюдения [ ${\displaystyle 0,T}$ ].

Задача обнаружения часто встречается в радиолокации и других областях радиотехники.

Различение сигналов

Допустим, что в принятом сигнале ${\displaystyle r(t)}$ может присутствовать только один из двух сигналов ${\displaystyle s_{1}(t,\lambda _{1})}$ и ${\displaystyle s_{2}(t,\lambda _{2})}$ , то есть принимаемый сигнал ${\displaystyle r(t)}$ равен

${\displaystyle r(t)=\alpha s_{1}(t,\lambda _{1})+(1-\alpha )s_{2}(t,\lambda _{2})+n(t)}$ ,

где ${\displaystyle \alpha }$ — случайная величина, которая может принимать значения 1 или 0. Если ${\displaystyle \alpha =1}$ , то в ${\displaystyle r(t)}$ с вероятностью ${\displaystyle p_{1}}$ присутствует сигнал ${\displaystyle s_{1}(t,\lambda _{1})}$ ; если ${\displaystyle \alpha }$ =0 , то в ${\displaystyle r(t)}$ с вероятностью ${\displaystyle p_{2}}$ присутствует сигнал ${\displaystyle s_{2}(t,\lambda _{2})}$ . В данном случае оценка параметра ${\displaystyle \alpha }$ является задачей различения двух сигналов. Задача различения более двух сигналов может быть сформулирована аналогично.

Если все кроме одного сигнала нулевые, то задача различения сигналов сводится к задаче обнаружения сигнала.

Задача различения сигналов часто встречается в радиосвязи и других областях радиотехники.

Оценка параметров сигнала

Если параметр сигнала ${\displaystyle \lambda }$ — случайная величина с априорной плотностью вероятности, то задачей оценки параметра сигнала является определение значения этого параметра с наименьшей погрешностью. Если требуется оценить несколько параметров сигнала, то такая задача называется совместной оценкой параметров сигнала.

Оценка параметров сигнала часто возникает в радиолокации , радионавигация и других областях радиотехники.

Фильтрация сообщений

Если параметр сигнала ${\displaystyle \lambda }$ случайно меняется на интервале наблюдения и является информационным сообщением ${\displaystyle \lambda (t)}$ , то есть случайным процессом с известными статистическими характеристиками, то задачей фильтрации является определение ${\displaystyle \lambda (t)}$ с наименьшей погрешностью. В общем случае информационных сообщений может быть несколько.

Задача фильтрации часто возникает в радиосвязи и телеметрии .

Разрешение сигналов

Задача разрешения сигналов подразумевает одновременное наличие в аддитивной смеси двух или более сигналов, разделяющих один и тот же частотный и временной ресурс. Разрешением в данных условиях будет называться оценка дискретных и непрерывных параметров каждого из сигналов, входящих в смесь.

Распознавание образов

При распознавании образов выявляется принадлежность рассматриваемого объекта (предмета, явления, сигнала и др.) к одному из заранее известных классов.

Примечания

Литература

• Перов А. И. (д.т.н). Статистическая теория радиотехнических систем / Рецезенты: д.т.н. профессор Юдин В.Н., к.т.н. профессор Бонч-Бруевич А. М.. — Учебник для ВУЗов. — М.:: Радиотехника, 2003. — 400 с. — ISBN 5-93108-047-3 .
• Тихонов В. И. Оптимальный приём сигналов / Под ред. А. Б. Васильева (Рецензенты: доктор технических наук, профессор — И.Н. Амиантов, доктор технических. наук проф. Б. Н. Митящев). — М. : Радио и связь, 1983. — 320 с.
• Трифонов А. П., Нечаев Е.П., Парфёнов В.И. Обнаружение стохастических сигналов с неизвестными параметрами / Под ред. А. П. Трифонова (Рецензенты: ). — монография. — Воронеж: Воронежский государственный университет, 1991. — 246 с. — ISBN 5-7555-9278.
• Фалькович. С.Е. Оценка параметров сигнала. — монография. — Москва: Советское радио, 1970. — 336 с.